题目内容
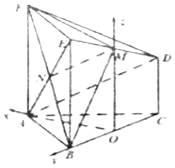
【题目】在如图所示的几何体中,正方形![]() 所在的平面与正三角形ABC所在的平面互相垂直,
所在的平面与正三角形ABC所在的平面互相垂直, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
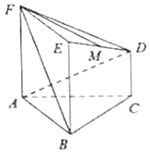
(1)求证: ![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:证明线面平则只需在平面内找一线与之平行即可,通常找中位线和建立平行四边形来证明,本题中可以容易发现连接AE交BF于点N,连接MN,可证MN为中位线;(2)二面角的问题通常借助于空间坐标系来求解,本题中可建立如图的坐标系,然后求出各面的法向量,再根据向量的夹角公式即可得出结论
解析:(1)连接AE交BF于点N,连接MN.
因为ABEF是正方形,所以N是AE的中点,
又M是ED的中点,所以MN∥AD.
因为AD平面BFM,MN![]() 平面BFM,
平面BFM,
所以AD∥平面BFM.
(2)因为ABEF是正方形,所以BE⊥AB,
因为平面ABEF⊥平面ABC,平面ABEF∩平面ABC=AB,
所以BE⊥平面ABC,因为CD∥BE,所以取BC的中点O,
连接OM,则OM⊥平面ABC,因为△ABC是正三角形,所以OA⊥BC,
所以以O为坐标原点建立如图所示的空间直角坐标系:
设CD=1,则B(0,1,0),E(0,1,2),D(0,﹣1,1),
![]() ,
,![]() .
.
设平面BMF的一个法向量为![]() ,
,
则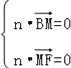 ,所以
,所以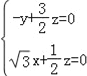 ,
,
令![]() ,则z=﹣6,y=﹣9,所以
,则z=﹣6,y=﹣9,所以![]() .
.
又因为![]() 是平面BME的法向量,
是平面BME的法向量,
所以![]() .
.
所以二面角E﹣BM﹣F的余弦值为![]() .
.

练习册系列答案
相关题目