题目内容
【题目】某学校为了解该校教师对教工食堂的满意度情况,随机访问了![]() 名教师.根据这
名教师.根据这![]() 名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为:
名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为: ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() .
.
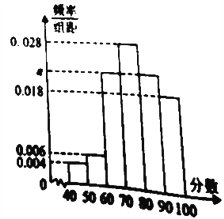
(1)求频率分布直方图中![]() 的值;
的值;
(2)从评分在![]() 的受访教师中,随机抽取2人,求此2人的评分都在
的受访教师中,随机抽取2人,求此2人的评分都在![]() 的概率.
的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据频率分布直方图的性质可知各频率之和为1即可得a=0.022;(2)先计算出受访教师中评分在[50,60)的人数:50×0.006×10=3(人),然后列出所有组合可能即可
解析:(1)因为(0.004+0.006+0.018+a×2+0.028)×10=1,
所以a=0.022
(2)受访教师中评分在[50,60)的有:
50×0.006×10=3(人),记为A1,A2,A3;
受访教师中评分在[40,50)的有:50×0.004×10=2(人),记为B1,B2…8分
从这5名受访教师中随机抽取2人,所有可能的结果共有10种,它们是{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A2,A3},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2}.
又因为所抽取2人的评分都在[50,60)的结果有3种,即{A1,A2},{A1,A3},{A2,A3},故所求的概率为![]() .
.

练习册系列答案
相关题目