题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若对任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时, ![]() 在
在![]() 为增函数,
为增函数, ![]() 在
在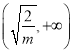 为减函数;当
为减函数;当![]() 时,
时, ![]() 在
在![]() 为增函数,在
为增函数,在 为减函数;(2)
为减函数;(2)![]() .
.
【解析】试题分析:(1)先求出函数导数![]() ,根据导函数符号的判定来下结论,因为此时导函数分子带参数无法确定符号,故进行讨论,通常根据参数大于0,等于0,小于0一一讨论定号即可得出单调性,但要注意定义域的限制;(2)恒成立问题通常转化最值问题求解,求参数取值范围我们一般会优先考虑参数分离形成新函数求最值,本题即可
,根据导函数符号的判定来下结论,因为此时导函数分子带参数无法确定符号,故进行讨论,通常根据参数大于0,等于0,小于0一一讨论定号即可得出单调性,但要注意定义域的限制;(2)恒成立问题通常转化最值问题求解,求参数取值范围我们一般会优先考虑参数分离形成新函数求最值,本题即可![]() 在
在![]() 上恒成立, 即
上恒成立, 即![]() 在
在![]() 上恒成立。,接下来分析函数
上恒成立。,接下来分析函数 ![]() 在
在![]() 上的最大值即可得出结论
上的最大值即可得出结论
解析:(1)由题知: ![]() ,
,
当m≤0时, ![]() >0在x∈(0,+∞)时恒成立,
>0在x∈(0,+∞)时恒成立,
∴f(x)在(0,+∞)上是增函数.
当m>0时, 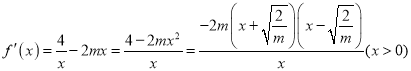 ,
,
令f′(x)>0,则![]() ;令f′(x)<0, 则
;令f′(x)<0, 则![]() .
.
∴f(x)在![]() 为增函数,f(x)在
为增函数,f(x)在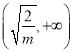 为减函数.
为减函数.
(2)法一:由题知: ![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立。
上恒成立。
令![]() ,所以
,所以 ![]()
令g′(x)>0,则![]() ;令g′(x)<0,则
;令g′(x)<0,则![]() .
.
∴g(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴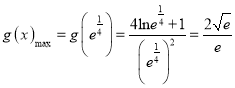 ,∴
,∴![]() .
.
法二:要使f(x) ≤0恒成立,只需![]() ,
,
(1)当m≤0时,f(x)在[1,e]上单调递增,所以 ![]() ,
,
即![]() ,这与m≤0矛盾,此时不成立.
,这与m≤0矛盾,此时不成立.
(2)当m>0时,
① 若![]() 即
即![]() 时,f(x)在[1,e]上单调递增,
时,f(x)在[1,e]上单调递增,
所以![]() ,即
,即![]() , 这与
, 这与![]() 矛盾,此时不成立.
矛盾,此时不成立.
②若1< ![]() 即
即![]() 时,f(x)在
时,f(x)在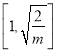 上单调递增,在
上单调递增,在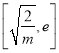 上单调递减 .
上单调递减 .
所以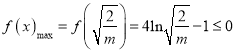 即
即![]() ,
,
解得 ![]() ,又因为
,又因为![]() ,所以
,所以 ![]() ,
,
③![]() 即m
即m![]() 2时,f(x)在
2时,f(x)在![]() 递减,则
递减,则![]() ,
,
∴![]() 又因为
又因为![]() ,所以m
,所以m![]() 2,综上
2,综上![]() .
.

练习册系列答案
相关题目