Question

【题目】已知数列{an}的通项公式an=5﹣n，其前n项和为Sn ， 将数列{an}的前4项抽去其中一项后，剩下三项按原来顺序恰为等比数列{bn}的前3项，记{bn}的前n项和为Tn ， 若存在m∈N* ， 使对任意n∈N* ， 总有Sn＜Tn+λ恒成立，则实数λ的取值范围是（ ）
A.λ≥2
B.λ＞3
C.λ≥3
D.λ＞2

Answer 1

【答案】D
【解析】解：∵an=5﹣n，
∴a1=4，a2=3，a3=2，a4=1，
则b1=a1=4，b2=a3=2，b3=a4=1，
∴数列{bn}是首项为4、公比为 的等比数列，
∴Tn= =8（1﹣ ），
∴4≤Tn＜8，
又∵Sn= = ，
∴当n=4或n=5时，Sn取最大值10，
∵存在m∈N* ， 使对任意n∈N* ， 总有Sn＜Tn+λ恒成立，
∴10＜8+λ，即λ＞2，
故选：D．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系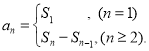才能正确解答此题．