题目内容
15.已知数列{an}中,a1=2,an>0(n∈N*),数列{an}的前n项和为Sn,且满足an+1=$\frac{2}{{{S_{n+1}}+{S_n}-2}}$.(1)判断数列{(Sn-1)2}是否等差数列或等比数列?试说明理由;
(2)设{bn}是数列{Sn}中的按从小到大顺序组成的整数数列.
①求b3;
②存在N(N∈N*),当n≤N时,使得在{Sn}中,数列{bn}有且只有20项,求N的范围.
分析 (1){(Sn-1)2}是等差数列,证明如下:由an+1=Sn+1-Sn,可得(Sn+1-Sn)(Sn+1+Sn-2)=2; 化简整理即可证明;
(2)由(1)知:(Sn-1)2=1+2(n-1)=2n-1,可得Sn=1+$\sqrt{2n-1}$.可得:S1=1+1=2=b1,S5=1+3=4=b2,S13=1+5=6=b3.由2n-1是奇数,Sn=1+$\sqrt{2n-1}$为有理数,可设n=2k2-2k+1,n递增,又当k=20时,n=761;当k=21时,n=841,即可得出.
解答 解:(1){(Sn-1)2}是等差数列,证明如下:
∵an+1=Sn+1-Sn,∴(Sn+1-Sn)(Sn+1+Sn-2)=2;
即(Sn+1)2-(Sn)2-2(Sn+1-Sn)=2,
∴(Sn+1-1)2-(Sn-1)2=2,且(S1-1)2=1,
∴{(Sn-1)2}是首项为1,公差为2的等差数列.
(2)由(1)知:(Sn-1)2=1+2(n-1)=2n-1,
∵an>0,
∴Sn≥an-1,∴Sn=1+$\sqrt{2n-1}$.
①n=1时,S1=1+1=2=b1,
n=5时,S5=1+3=4=b2,
n=13时,S13=1+5=6=b3.
②∵2n-1是奇数,Sn=1+$\sqrt{2n-1}$为有理数,则$\sqrt{2n-1}$=2k-1,k∈Z.
∴n=2k2-2k+1,
当k≥1时,n递增,又当k=20时,n=761;当k=21时,n=841;
∴存在N∈[761,840],当n≤N时,使得在{Sn}中,数列{bk}有且只有20项.
点评 本题考查了等差数列的通项公式、递推式的应用、数列的单调性,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.等差数列{an},{bn}的前n项和分别为Sn,Tn,若$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n+4}{3n+1}$,则an=bn时n=( )
| A. | 2 | B. | 6 | C. | 无解 | D. | 无数多个 |
7. 正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )
正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )
 正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )
正整数按下表的规律排列(下表给出的是上起前4行和左起前4列)则上起第2015行,左起第2016列的数应为( )| A. | 20152 | B. | 20162 | C. | 2015+2016 | D. | 2015×2016 |
5.若点P在平面ABC内射影为O,且PA⊥BC,PB⊥AC,则点O为△ABC的( )
| A. | 重心 | B. | 外心 | C. | 内心 | D. | 垂心 |
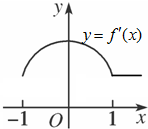 已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象可能是( )
已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如图所示,则该函数的图象可能是( )