题目内容
12.如图,一个正三棱柱的左视图是边长为$\sqrt{3}$的正方形,则它的外接球的表面积等于( )
| A. | 8π | B. | $\frac{25π}{3}$ | C. | 9π | D. | $\frac{28π}{3}$ |
分析 由题意可得:正三棱柱的高是$\sqrt{3}$,底面正三角的高也是$\sqrt{3}$.设球心为O,半径为R,△ABC的中心为G,所以△OGA是直角三角形,OG是高的一半,OG=$\frac{\sqrt{3}}{2}$,所以GA=$\frac{2\sqrt{3}}{3}$.在△OAG中由勾股定理得:R2=$\frac{25}{12}$.进而得到答案
解答 解:因为正三棱柱ABC-DEF的正视图是边长为$\sqrt{3}$的正方形,
所以正三棱柱的高是$\sqrt{3}$,底面正三角的高也是$\sqrt{3}$.
设它的外接球的球心为O,半径为R,底面△ABC的中心为G,
所以△OGA是直角三角形,OG是高的一半,OG=$\frac{\sqrt{3}}{2}$,
GA是正三角形ABC的高的$\frac{2}{3}$,
所以GA=$\frac{2\sqrt{3}}{3}$.
在△OAG中由勾股定理得:R2=OG2+GA2
解得:R2=$\frac{25}{12}$.
∴球的表面积为4πR2=$\frac{25π}{3}$.
故选:B
点评 解决此类问题的关键是熟练掌握几何体的结构特征与及球的定义,在球的内接多面体中一般容易出现直角三角形,进而利用勾股定理解决问题即可.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
7.在△ABC中,角A、B、C所对的边分别是a、b、c,满足acosA+bcosB=ccosC,则△ABC为( )
| A. | 等边三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 直角三角形 |
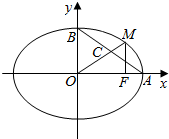 如图所示,A,B分别是椭圆的右、上顶点,C是AB的三等分点(靠近点B),F为椭圆的右焦点,OC的延长线交椭圆于点M,且MF⊥OA,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.
如图所示,A,B分别是椭圆的右、上顶点,C是AB的三等分点(靠近点B),F为椭圆的右焦点,OC的延长线交椭圆于点M,且MF⊥OA,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.