题目内容
17.已知函数f(x)=$\frac{2x+3}{3x}$,数列{an}满足${a_1}=1,{a_{n+1}}=f(\frac{1}{a_n}),(n∈{N^*})$(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{{a_{n-1}}{a_n}}}(n≥2),{b_1}$=3,数列{bn}的前n项和为Sn,证明:对一切n∈N*,都有Sn<$\frac{9}{2}$.
分析 (1)由已知得${a}_{n+1}=\frac{\frac{2}{{a}_{n}}+3}{\frac{3}{{a}_{n}}}$=$\frac{2+3{a}_{n}}{3}$=${a}_{n}+\frac{2}{3}$,从而数列{an}是首项为1,公差为$\frac{2}{3}$的等差数列,由此能求出数列{an}的通项公式.
(2)n≥2时,bn=$\frac{1}{(\frac{2}{3}n-\frac{1}{3})(\frac{2}{3}n+\frac{1}{3})}$=$\frac{9}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,${b}_{1}=3=\frac{9}{2}(1-\frac{1}{3})$,由此利用裂项求和法能证明对一切n∈N*,都有Sn<$\frac{9}{2}$.
解答 (1)解:∵函数f(x)=$\frac{2x+3}{3x}$,数列{an}满足${a_1}=1,{a_{n+1}}=f(\frac{1}{a_n}),(n∈{N^*})$,
∴${a}_{n+1}=\frac{\frac{2}{{a}_{n}}+3}{\frac{3}{{a}_{n}}}$=$\frac{2+3{a}_{n}}{3}$=${a}_{n}+\frac{2}{3}$,
∴数列{an}是首项为1,公差为$\frac{2}{3}$的等差数列,
∴${a}_{n}=1+(n-1)×\frac{2}{3}$=$\frac{2}{3}n+\frac{1}{3}$.
(2)证明:∵bn=$\frac{1}{{{a_{n-1}}{a_n}}}(n≥2),{b_1}$=3,
∴n≥2时,bn=$\frac{1}{(\frac{2}{3}n-\frac{1}{3})(\frac{2}{3}n+\frac{1}{3})}$=$\frac{9}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
又${b}_{1}=3=\frac{9}{2}(1-\frac{1}{3})$,
∴${S}_{n}=\frac{9}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{2n-1}-\frac{1}{2n+1})$
=$\frac{9}{2}(1-\frac{1}{2n+1})$
=$\frac{9}{2}-\frac{9}{4n+2}$<$\frac{9}{2}$,
∴对一切n∈N*,都有Sn<$\frac{9}{2}$.
点评 本题考查数列的通项公式的证明,考查数列的前n项和小于$\frac{9}{2}$的证明,是中档题,解题时要认真等差数列和裂项求和法的合理运用.

 阅读快车系列答案
阅读快车系列答案
| A. | 8π | B. | $\frac{25π}{3}$ | C. | 9π | D. | $\frac{28π}{3}$ |
| A. | x+y=2 | B. | x+y=1 | C. | x=1或y=1 | D. | x+y=2或x-y=0 |
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
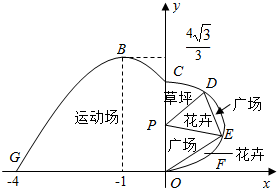 如图,我市体育公园的运动休闲区域的平面图如图所示,在y轴左侧的运动区的边界曲线段是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,$\frac{4\sqrt{3}}{3}$),在y轴右侧的休闲区的边界曲线段是以P为圆心,CO为直径的半圆弧,D、E两点在半圆弧上,满足$\widehat{CE}$=$\widehat{DE}$.
如图,我市体育公园的运动休闲区域的平面图如图所示,在y轴左侧的运动区的边界曲线段是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,$\frac{4\sqrt{3}}{3}$),在y轴右侧的休闲区的边界曲线段是以P为圆心,CO为直径的半圆弧,D、E两点在半圆弧上,满足$\widehat{CE}$=$\widehat{DE}$.