题目内容
2.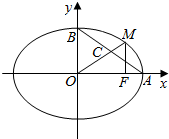 如图所示,A,B分别是椭圆的右、上顶点,C是AB的三等分点(靠近点B),F为椭圆的右焦点,OC的延长线交椭圆于点M,且MF⊥OA,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.
如图所示,A,B分别是椭圆的右、上顶点,C是AB的三等分点(靠近点B),F为椭圆的右焦点,OC的延长线交椭圆于点M,且MF⊥OA,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.
分析 设A(a,0),B(0,b),F(c,0),椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),求得C和M的坐标,运用O,C,M共线,即有kOC=kOM,再由离心率公式计算即可得到所求值.
解答 解:设A(a,0),B(0,b),F(c,0),
椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
令x=c,可得y=b$\sqrt{1-\frac{{c}^{2}}{{a}^{2}}}$=$\frac{{b}^{2}}{a}$,
即有M(c,$\frac{{b}^{2}}{a}$),
由C是AB的三等分点(靠近点B),
可得C($\frac{a}{1+2}$,$\frac{2b}{1+2}$),即($\frac{a}{3}$,$\frac{2b}{3}$),
由O,C,M共线,可得kOC=kOM,
即为$\frac{2b}{a}$=$\frac{{b}^{2}}{ac}$,即有b=2c,
a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{5}$c,则e=$\frac{c}{a}$=$\frac{\sqrt{5}}{5}$.
故答案为:$\frac{\sqrt{5}}{5}$.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率的求法,注意运用直线的有关知识,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.函数f(x)=log3(4x-1)的定义域为( )
| A. | (-∞,$\frac{1}{2}$] | B. | [$\frac{1}{2},+∞$) | C. | ($\frac{1}{4},\frac{1}{2}$] | D. | ($\frac{1}{4},+∞$) |
14.已知函数f(x)=ax2-1的图象在点A(1,f(1))处的切线l与直线8x-y+2=0平行,若数列{$\frac{1}{f(n)}$}的前n项和为Sn,则S2015的值为( )
| A. | $\frac{4030}{4031}$ | B. | $\frac{2014}{4029}$ | C. | $\frac{2015}{4031}$ | D. | $\frac{4030}{4031}$ |
12.如图,一个正三棱柱的左视图是边长为$\sqrt{3}$的正方形,则它的外接球的表面积等于( )


| A. | 8π | B. | $\frac{25π}{3}$ | C. | 9π | D. | $\frac{28π}{3}$ |
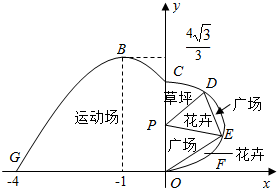 如图,我市体育公园的运动休闲区域的平面图如图所示,在y轴左侧的运动区的边界曲线段是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,$\frac{4\sqrt{3}}{3}$),在y轴右侧的休闲区的边界曲线段是以P为圆心,CO为直径的半圆弧,D、E两点在半圆弧上,满足$\widehat{CE}$=$\widehat{DE}$.
如图,我市体育公园的运动休闲区域的平面图如图所示,在y轴左侧的运动区的边界曲线段是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),x∈[-4,0]时的图象且最高点B(-1,$\frac{4\sqrt{3}}{3}$),在y轴右侧的休闲区的边界曲线段是以P为圆心,CO为直径的半圆弧,D、E两点在半圆弧上,满足$\widehat{CE}$=$\widehat{DE}$.