题目内容
设函数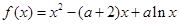 ,其中
,其中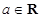 .
.
(Ⅰ)若函数 的图象在点
的图象在点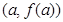 处的切线与直线
处的切线与直线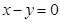 平行,求实数
平行,求实数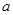 的值;
的值;
(Ⅱ)求函数 的极值.
的极值.
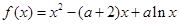 ,其中
,其中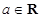 .
. (Ⅰ)若函数
 的图象在点
的图象在点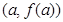 处的切线与直线
处的切线与直线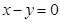 平行,求实数
平行,求实数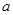 的值;
的值;(Ⅱ)求函数
 的极值.
的极值.(Ⅰ)解:函数 的定义域是
的定义域是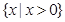 . ……………… 1分
. ……………… 1分
对 求导数,得
求导数,得 . ………… 3分
. ………… 3分
由题意,得 ,且
,且 ,
,
解得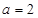 . ………………………… 5分
. ………………………… 5分
(Ⅱ)解:由 ,得方程
,得方程 ,
,
一元二次方程 存在两解
存在两解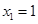 ,
,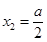 ,………… 6分
,………… 6分
当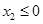 时,即当
时,即当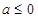 时,
时,
随着x的变化, 与
与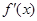 的变化情况如下表:
的变化情况如下表:
即函数 在
在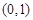 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
所以函数 在
在 存在极小值
存在极小值 ; …………… 8分
; …………… 8分
当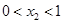 时,即当
时,即当 时,
时,
随着x的变化, 与
与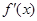 的变化情况如下表:
的变化情况如下表:
即函数 在
在 ,
, 上单调递增,在
上单调递增,在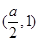 上单调递减.
上单调递减.
所以函数 在
在 存在极小值
存在极小值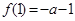 ,在
,在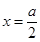 存在极大值
存在极大值 ; ………………………… 10分
; ………………………… 10分
当 时,即当
时,即当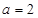 时,
时,
因为 (当且仅当
(当且仅当 时等号成立),
时等号成立),
所以 在
在 上为增函数,故不存在极值; ……………12分
上为增函数,故不存在极值; ……………12分
当 时,即当
时,即当 时,
时,
随着x的变化, 与
与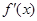 的变化情况如下表:
的变化情况如下表:
即函数 在
在 ,
,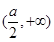 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
所以函数 在
在 存在极大值
存在极大值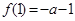 ,在
,在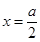 存在极小值
存在极小值 ;
;
综上,当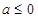 时,函数
时,函数 存在极小值
存在极小值 ,不存在极大值;
,不存在极大值;
当 时,函数
时,函数 存在极小值
存在极小值 ,存在极大值
,存在极大值 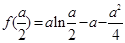 ;
;
当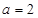 时,函数
时,函数 不存在极值;
不存在极值;
当 时,函数
时,函数 存在极大值
存在极大值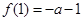 ,存在极小值
,存在极小值 .
.
 的定义域是
的定义域是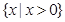 . ……………… 1分
. ……………… 1分对
 求导数,得
求导数,得 . ………… 3分
. ………… 3分由题意,得
 ,且
,且 ,
,解得
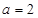 . ………………………… 5分
. ………………………… 5分(Ⅱ)解:由
 ,得方程
,得方程 ,
,一元二次方程
 存在两解
存在两解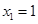 ,
,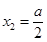 ,………… 6分
,………… 6分当
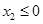 时,即当
时,即当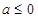 时,
时,随着x的变化,
 与
与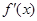 的变化情况如下表:
的变化情况如下表: 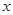 |  | 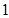 | 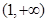 |
 | 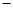 |  |  |
 | ↘ | 极小值 | ↗ |
 在
在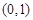 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.所以函数
 在
在 存在极小值
存在极小值 ; …………… 8分
; …………… 8分当
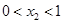 时,即当
时,即当 时,
时,随着x的变化,
 与
与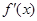 的变化情况如下表:
的变化情况如下表: 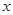 |  |  | 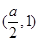 | 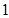 | 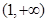 |
 |  |  | 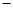 |  |  |
 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
 在
在 ,
, 上单调递增,在
上单调递增,在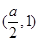 上单调递减.
上单调递减.所以函数
 在
在 存在极小值
存在极小值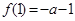 ,在
,在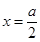 存在极大值
存在极大值 ; ………………………… 10分
; ………………………… 10分当
 时,即当
时,即当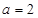 时,
时,因为
 (当且仅当
(当且仅当 时等号成立),
时等号成立),所以
 在
在 上为增函数,故不存在极值; ……………12分
上为增函数,故不存在极值; ……………12分当
 时,即当
时,即当 时,
时,随着x的变化,
 与
与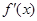 的变化情况如下表:
的变化情况如下表: 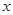 |  | 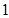 |  |  | 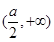 |
 |  |  | 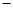 |  |  |
 | 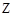 | 极大值 | 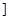 | 极小值 | 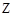 |
 在
在 ,
,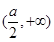 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.所以函数
 在
在 存在极大值
存在极大值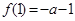 ,在
,在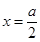 存在极小值
存在极小值 ;
;综上,当
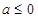 时,函数
时,函数 存在极小值
存在极小值 ,不存在极大值;
,不存在极大值;当
 时,函数
时,函数 存在极小值
存在极小值 ,存在极大值
,存在极大值 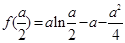 ;
;当
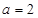 时,函数
时,函数 不存在极值;
不存在极值;当
 时,函数
时,函数 存在极大值
存在极大值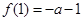 ,存在极小值
,存在极小值 .
.本试题主要是考查了导数的几何意义的运用,以及运用到导数求解函数极值的综合运用
(1)先分析定义域,然后求解导数得到再给定点的导数值,进而确定切线方程 。
(2)需要对参数a进行分类讨论,判定单调性,进而得到不同情况下的极值问题。
(1)先分析定义域,然后求解导数得到再给定点的导数值,进而确定切线方程 。
(2)需要对参数a进行分类讨论,判定单调性,进而得到不同情况下的极值问题。

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 .
. ,求
,求 的单调区间;
的单调区间; 是
是 ,若
,若 恒成立,求实数b的取值范围.
恒成立,求实数b的取值范围.  。
。 

 时,
时, 恒成立。
恒成立。 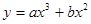 ,当
,当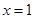 时,有极大值
时,有极大值 ;
;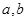 的值;(2)求函数
的值;(2)求函数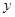 的极小值。
的极小值。 是定义在
是定义在 上的可导函数,且满足
上的可导函数,且满足 . 若
. 若 且
且 ,则
,则



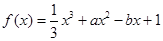 (
(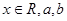 为实数)有极值,且在
为实数)有极值,且在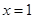 处的切线与直线
处的切线与直线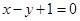 平行.
平行.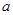 的取值范围;
的取值范围;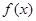 的极小值为
的极小值为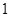 ,若存在,求出实数
,若存在,求出实数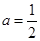 ,
,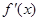 ,令
,令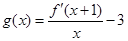
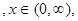
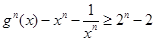
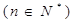
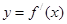 的图象,那么函数
的图象,那么函数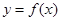 在下面哪个区间是减函数( )
在下面哪个区间是减函数( )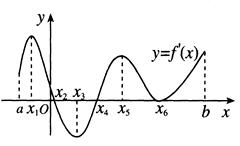
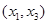

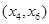
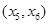
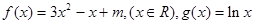
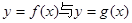 有公共切线时,求函数
有公共切线时,求函数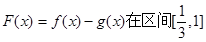 上的最值
上的最值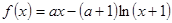 ,其中
,其中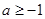 ,求
,求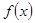 的单调区间。
的单调区间。