题目内容
设函数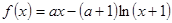 ,其中
,其中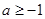 ,求
,求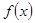 的单调区间。
的单调区间。
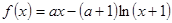 ,其中
,其中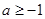 ,求
,求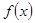 的单调区间。
的单调区间。 当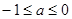 时
时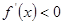 ,函数
,函数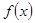 在
在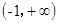 上单调递减;
上单调递减;
当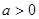 时,由
时,由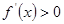 得
得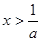 ,
,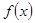 在
在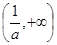 上单调递增
上单调递增
由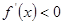 得
得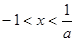 ,
,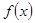 在
在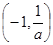 上单调递减
上单调递减
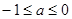 时
时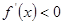 ,函数
,函数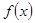 在
在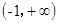 上单调递减;
上单调递减;当
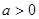 时,由
时,由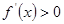 得
得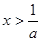 ,
,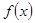 在
在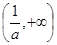 上单调递增
上单调递增由
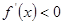 得
得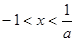 ,
,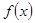 在
在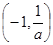 上单调递减
上单调递减本试题主要考查了导数在研究函数中的运用。利用导数判定函数单调区间,先求解定义域,然后分析导数为零的点,然后解不等式,得到导数大于零和小于零的解集,从而得到单调区间的问题。注意回答问题用区间表示。
函数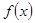 的定义域是
的定义域是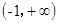 ,
,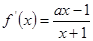
当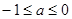 时
时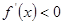 ,函数
,函数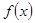 在
在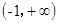 上单调递减;
上单调递减;
当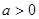 时,由
时,由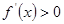 得
得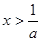 ,
,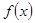 在
在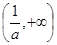 上单调递增
上单调递增
由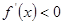 得
得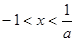 ,
,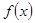 在
在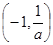 上单调递减
上单调递减
函数
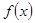 的定义域是
的定义域是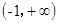 ,
,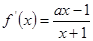
当
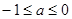 时
时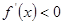 ,函数
,函数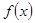 在
在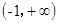 上单调递减;
上单调递减;当
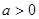 时,由
时,由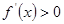 得
得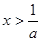 ,
,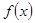 在
在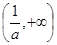 上单调递增
上单调递增由
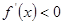 得
得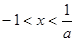 ,
,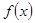 在
在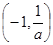 上单调递减
上单调递减
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
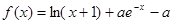 ,
,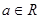 .
.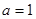 时,证明
时,证明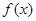 在
在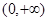 是增函数;
是增函数;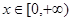 ,
,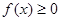 ,求
,求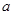 的取值范围.
的取值范围.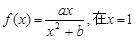 处取得极值为2.
处取得极值为2.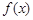 的解析式;
的解析式;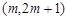 上为增函数,求实数m的取值范围;
上为增函数,求实数m的取值范围;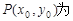
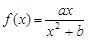 图象上的任意一点,直线l与
图象上的任意一点,直线l与 的图象相切于点P,求直线l的斜率的取值范围.
的图象相切于点P,求直线l的斜率的取值范围.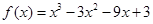 ,若函数
,若函数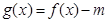 在
在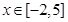 上有3个零点,求实数
上有3个零点,求实数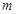 的取值范围.
的取值范围.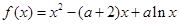 ,其中
,其中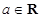 .
.  的图象在点
的图象在点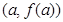 处的切线与直线
处的切线与直线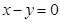 平行,求实数
平行,求实数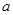 的值;
的值;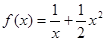 ,存在
,存在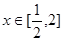 ,使得
,使得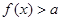 成立,则实数
成立,则实数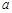 的取值范围是( )
的取值范围是( )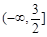
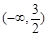

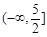
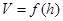 。
。
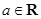 ,函数
,函数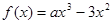
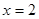 是函数
是函数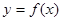 的极值点,求实数
的极值点,求实数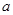 的值;
的值;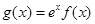 在
在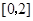 上是单调减函数,求实数
上是单调减函数,求实数