题目内容
设 是定义在
是定义在 上的可导函数,且满足
上的可导函数,且满足 . 若
. 若 且
且 ,则
,则
 是定义在
是定义在 上的可导函数,且满足
上的可导函数,且满足 . 若
. 若 且
且 ,则
,则A. | B. |
C. | D. |
A
解:xf′(x)+f(x)≤0⇒[xf(x)]′≤0⇒函数F(x)=xf(x)在(0,+∞)上为常函数或递减,
又0<a<b且f(x)非负,于是有:af(a)≥bf(b)≥0①1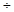 a2>1
a2>1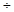 b2>0②
b2>0②
①②两式相乘得:f(a)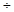 a ≥f(b)
a ≥f(b)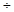 b ≥0⇒af(b)≤bf(a),故选A.
b ≥0⇒af(b)≤bf(a),故选A.
又0<a<b且f(x)非负,于是有:af(a)≥bf(b)≥0①1
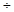 a2>1
a2>1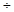 b2>0②
b2>0②①②两式相乘得:f(a)
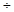 a ≥f(b)
a ≥f(b)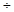 b ≥0⇒af(b)≤bf(a),故选A.
b ≥0⇒af(b)≤bf(a),故选A.
练习册系列答案
相关题目
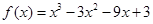 ,若函数
,若函数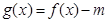 在
在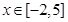 上有3个零点,求实数
上有3个零点,求实数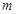 的取值范围.
的取值范围.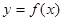 在定义域(-
在定义域(-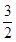 ,3)内可导,其图象如图所示,记
,3)内可导,其图象如图所示,记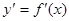 ,则不等式
,则不等式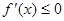 的解集为( )
的解集为( )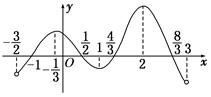
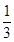 ,1]∪[2,3)
,1]∪[2,3) ]∪[
]∪[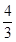 ,
,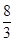 ]
]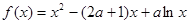
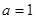 时, 求函数
时, 求函数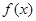 的单调增区间;
的单调增区间;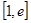 上的最小值;
上的最小值;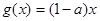 ,若存在
,若存在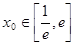 ,使得
,使得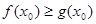 成立,求实数
成立,求实数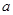 的取值范围.
的取值范围. .
. 是函数
是函数 的极值点,求
的极值点,求 的值;
的值;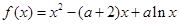 ,其中
,其中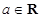 .
.  的图象在点
的图象在点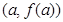 处的切线与直线
处的切线与直线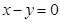 平行,求实数
平行,求实数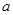 的值;
的值;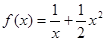 ,存在
,存在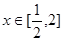 ,使得
,使得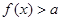 成立,则实数
成立,则实数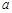 的取值范围是( )
的取值范围是( )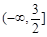
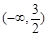

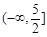
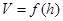 。
。