题目内容
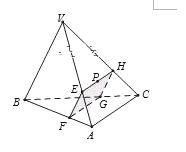
【题目】如图所示,在四面体VABC木块中,P为△VAC的重心,这点P作截面EFGH,若截面EFGH是平行四边形,则该截面把木块分成两部分体积之比为____________. (填体积小与体积大之比)
【答案】![]()
【解析】
由![]() ,且
,且![]() ,连接
,连接![]() ,则多面体
,则多面体![]() 的体积等于四棱锥
的体积等于四棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积之和,多面体
的体积之和,多面体![]() 的体积等于四棱锥
的体积等于四棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积和,找出多面体的体积的关系,得到答案.
的体积和,找出多面体的体积的关系,得到答案.
如图,因为四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() ,则
,则![]() ,
,
因为P为![]() 的中心,所以
的中心,所以![]() ,
,
而![]() ,所以
,所以![]() ,
,
连接![]() ,
,
则多面体![]() 的体积等于四棱锥
的体积等于四棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积和,
的体积和,
多面体![]() 的体积等于四棱锥
的体积等于四棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积和.
的体积和.
因为四棱锥![]() 的高是四棱锥
的高是四棱锥![]() 的高的2倍,底面积相等,
的高的2倍,底面积相等,
所以四棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 的体积的2倍;
的体积的2倍;
因为三棱锥![]() 的底面是三棱锥
的底面是三棱锥![]() 的底面面积的
的底面面积的![]() 倍,高是3倍,
倍,高是3倍,
所以三棱锥![]() 的体积是三棱锥
的体积是三棱锥![]() 的体积的4倍,
的体积的4倍,
设论证![]() 的体积为
的体积为![]() ,则三棱锥
,则三棱锥![]() 的体积为
的体积为![]() ,四棱锥
,四棱锥![]() 的体积是
的体积是![]() ,所以多面体
,所以多面体![]() 的体积是
的体积是![]() ,
,
又多面体![]() 的体积等于
的体积等于![]() ,
,
所以多面体![]() 的体积与多面体
的体积与多面体![]() 的体积比等于
的体积比等于![]() .
.

练习册系列答案
相关题目
【题目】一个化肥厂生产甲种混合肥料1车皮、乙种混合肥料1车皮所需要的主要原料如表:
原料 | 磷酸盐(单位:吨) | 硝酸盐(单位:吨) |
甲 | 4 | 20 |
乙 | 2 | 20 |
现库存磷酸盐8吨、硝酸盐60吨,计划在此基础上生产若干车皮的甲、乙两种混合肥料.
(1)设x,y分别表示计划生产甲、乙两种肥料的车皮数,试列出x,y满足的数学关系式,并画出相应的平面区域;
(2)若生产1车皮甲种肥料,利润为3万元;生产1车皮乙种肥料,利润为2万元.那么分别生产甲、乙两种肥料多少车皮,能够产生最大利润?最大利润是多少?