题目内容
【题目】若函数y=f(x)在x=x0处取得极大值或极小值,则称x0为函数y=f(x)的极值点.已知a,b是实数,1和-1是函数f(x)=x3+ax2+bx的两个极值点.
(1)求a和b的值;
(2)设函数g(x)的导函数g′(x)=f(x)+2,求g(x)的极值点.
【答案】(1)a=0,b=-3.
(2)-2.
【解析】(1)由题设得f′(x)=3x2+2ax+b,
所以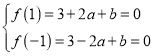 ,
,
解之得a=0,b=-3.
(2)由(1)知f(x)=x3-3x.
因为f(x)+2=(x-1)2(x+2),
所以g′(x)=0的根为x1=x2=1,x3=-2,
于是函数g(x)的极值点只可能是1或-2.
当x<-2时,g′(x)<0;当-2<x<1时,
g′(x)>0,故-2是g(x)的极值点.
当-2<x<1或x>1时,g′(x)>0,
故1不是g(x)的极值点.
所以g(x)的极值点为-2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目