题目内容
20.已知动圆C过定点(1,0)且与直线x=-1相切(1)求动圆圆心C的轨迹方程;
(2)设过定点M (-4,0)的直线?与圆心C的轨迹有两个交点A,B,坐标原点为O,设∠xOA=α,∠xOB=β,试探究α+β是否为定值,若是定值,求定值,若不是定值,说明理由.
分析 (1)设圆的圆心为(x,y),运用两点的距离和直线和圆相切的条件:d=r,化简整理,即可得到轨迹方程;
(2)设过定点M(-4,0)的直线l的方程为x=my-4,代入抛物线方程可得,y2-4my+16=0,设A($\frac{{{y}_{1}}^{2}}{4}$,y1),B($\frac{{{y}_{2}}^{2}}{4}$,y2),运用韦达定理和直线的斜率公式,计算即可得到定值.
解答 解:(1)设圆的圆心为(x,y),
由动圆C过定点(1,0)且与直线x=-1相切,
可得$\sqrt{(x-1)^{2}+{y}^{2}}$=|x+1|,
化简可得y2=4x;
(2)设过定点M(-4,0)的直线l的方程为x=my-4,
代入抛物线方程可得,y2-4my+16=0,
设A($\frac{{{y}_{1}}^{2}}{4}$,y1),B($\frac{{{y}_{2}}^{2}}{4}$,y2),
则y1+y2=4m,y1y2=16,
由题意当m>0,可得OA的斜率为k1=tanα=$\frac{4}{{y}_{1}}$,
OA的斜率为k2=tanβ=$\frac{4}{{y}_{2}}$,
即有tanαtanβ=1,
则α+β=90°;
当m<0时,同样有tanαtanβ=1,
则α+β=90°.
故α+β为定值,且为90°.
点评 本题考查轨迹方程的求法,同时考查直线和圆相切的条件,以及抛物线的方程的运用,联立直线方程,运用韦达定理,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
11.公元前3世纪,古希腊欧几里得在《几何原本》里提出:“球的体积(V)与它的直径(D)的立方成正比”,此即V=kD3,欧几里得未给出k的值.17世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式V=kD3中的常数k称为“立圆率”或“玉积率”.类似地,对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式V=kD3求体积(在等边圆柱中,D表示底面圆的直径;在正方体中,D表示棱长).假设运用此体积公式求得球(直径为a)、等边圆柱(底面圆的直径为a)、正方体(棱长为a)的“玉积率”分别为k1、k2、k3,那么k1:k2:k3( )
| A. | $\frac{1}{4}:\frac{1}{6}:\frac{1}{π}$ | B. | $\frac{π}{6}:\frac{π}{4}$:2 | C. | 2:3:2π | D. | $\frac{π}{6}:\frac{π}{4}$:1 |
15.已知f(x)=3x+2xf′(1),则曲线f(x)在x=0处的切线在x轴上的截距为( )
| A. | 1 | B. | 5ln3 | C. | -5ln3 | D. | $\frac{1}{5ln3}$ |
12.设随即变量X服从标准正态分布,已知P(X≤1.88)=0.97,则P(|X|≤1.88)=( )
| A. | 0.94 | B. | 0.97 | C. | 0.06 | D. | 0.03 |
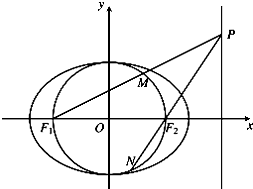 已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A(1,$\frac{\sqrt{2}}{2}$),其焦距为2.
已知椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点A(1,$\frac{\sqrt{2}}{2}$),其焦距为2.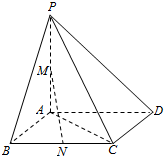 如图,四棱锥P-ABCD中,PA=AB=1,PA⊥底面ABCD,底面ABCD为正方形,且M,N分别为PA与BC的中点
如图,四棱锥P-ABCD中,PA=AB=1,PA⊥底面ABCD,底面ABCD为正方形,且M,N分别为PA与BC的中点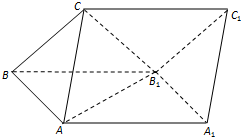 如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
如图,三棱柱ABC-A1B1C1的侧面ABB1A1为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C. 如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.
如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.