题目内容
18.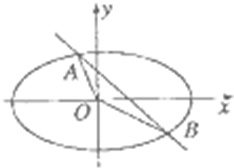 如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.
如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.(Ⅰ)若椭圆的焦距为2,离心率e=$\frac{\sqrt{3}}{3}$,求△OAB的面积;
(Ⅱ)若以A、B为直径的圆经过原点,且椭圆的长轴2a∈[$2\sqrt{2}$,$2\sqrt{3}$]时,求椭圆离心率取值范围.
分析 (Ⅰ)∵e=$\frac{\sqrt{3}}{3}$,2c=2,则$\frac{c}{a}=\frac{\sqrt{3}}{3}$,∴$a=\sqrt{3}$,则b=$\sqrt{{a}^{2}-{c}^{2}}=\sqrt{2}$.解得椭圆方程.
(Ⅱ)设A(x1,y1),B(x2,y2),由$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\\{y=-x+1}\end{array}\right.$,消去y得:(a2+b2)x2-2a2x+a2(1-b2)=0,由∵$\overrightarrow{OA}⊥\overrightarrow{OB}$,∴$\overrightarrow{OA}•\overrightarrow{OB}=0$,即x1x2+y1y2=0,代入列式求解.
解答 解:(Ⅰ)∵e=$\frac{\sqrt{3}}{3}$,2c=2,则$\frac{c}{a}=\frac{\sqrt{3}}{3}$,∴$a=\sqrt{3}$,则b=$\sqrt{{a}^{2}-{c}^{2}}=\sqrt{2}$.
∴椭圆得方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$
将y=-x+1代入消去y得:5x2-6x-3=0
设A(x1,y1),B(x2,y2)
∴$|AB|=\sqrt{1+(-1)^{2}}×\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}×\sqrt{(\frac{6}{5})^{2}+\frac{12}{5}}=\frac{8\sqrt{3}}{5}$,
又原点到直线l的距离d=$\frac{\sqrt{2}}{2}$,故${S}_{△AOB}=\frac{2\sqrt{6}}{5}$
(Ⅱ)设A(x1,y1),B(x2,y2)
∵$\overrightarrow{OA}⊥\overrightarrow{OB}$,∴$\overrightarrow{OA}•\overrightarrow{OB}=0$,即x1x2+y1y2=0
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\\{y=-x+1}\end{array}\right.$,消去y得:(a2+b2)x2-2a2x+a2(1-b2)=0
由△=(-2a2)2-4a2(a2+b2)(1-b2)>0,整理得a2+b2>1
又x1+x2=$\frac{2{a}^{2}}{{a}^{2}+{b}^{2}},{x}_{1}{x}_{2}=\frac{{a}^{2}(1-{b}^{2})}{{a}^{2}+{b}^{2}}$
y1y2=(-x1+1)(-x2+1)=x1x2-(x1+x2)+1
由x1x2+y1y2=0,得:2x1x2-(x1+x2)+1=0
∴$\frac{2{a}^{2}(1-{b}^{2})}{{a}^{2}+{b}^{2}}-\frac{2{a}^{2}}{{a}^{2}+{b}^{2}}+1=0$整理得:a2+b2-2a2b2=0,
∵b2=a2-c2=a2-a2e2代入上式得:2${a}^{2}=1+\frac{1}{1-{e}^{2}}$∴${e}^{2}=1-\frac{1}{2{a}^{2}-1}∴2a∈[2\sqrt{2},2\sqrt{3}]$
∴${e}^{2}∈[\frac{2}{3},\frac{4}{5}]$,符合条件a2+b2>1
由此得:$e∈[\frac{\sqrt{6}}{3},\frac{2\sqrt{5}}{5}]$
点评 本题主要考查了椭圆方程的求法和直线与圆锥曲线的综合问题属于中档题型,高考经常涉及.

 阅读快车系列答案
阅读快车系列答案| A. | $(-∞,\frac{1}{2}]$ | B. | $[{\frac{1}{5},\frac{1}{2}}]$ | C. | $[{\frac{1}{5},+∞})$ | D. | $(-∞,\frac{1}{5}]$ |
| A. | EF∥GH | B. | EH∥FG | C. | EH∥平面BCD | D. | FG∥平面ABD |
 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.