题目内容
15．已知f（x）=3x+2xf′（1），则曲线f（x）在x=0处的切线在x轴上的截距为（ ）| A． | 1 | B． | 5ln3 | C． | -5ln3 | D． | $\frac{1}{5ln3}$ |
分析 由题意求出f′（x）令x=1代入求出f′（1），可求出f（x）和f′（x）的表达式，再求出f（0）和f′（0）的值，代入点斜式方程化简求出切线方程，令y=0代入切线方程求出x的值即可．
解答 解：由题意知，f（x）=3x+2xf′（1），
∴f′（x）=（ln3）•3x+2f′（1），
令x=1代入上式得，f′（1）=（ln3）•3+2f′（1），
解得f′（1）=-3ln3，
∴f（x）=3x-6（ln3）x，f′（x）=（ln3）•3x-6ln3，
∴f（0）=1，f′（0）=ln3-6ln3=-5ln3，
则在x=0处的切线方程是y-1=-5ln3（x-0），即y=-5（ln3）x+1，
令y=0代入得，x=$\frac{1}{5ln3}$，
∴曲线f（x）在x=0处的切线在x轴上的截距为：$\frac{1}{5ln3}$，
故选：D．
点评 本题考查求导公式，导数的几何意义以及切线方程，以及直线的截距问题，是中档题．
练习册系列答案
相关题目
5．已知i为虚数单位，则复数$\frac{1-3i}{1+i}$=（ ）
| A． | 2+i | B． | 2-i | C． | -1-2i | D． | -1+i |
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，以原点为圆心，以椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切．
10．sin$\frac{5π}{12}$=（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{\sqrt{3}}{4}$ | C． | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D． | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
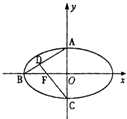如图，椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率e=$\frac{3}{5}$，左焦点为F，A，B，C为其三个顶点，直线CF与AB交于点D，若△ADC的面积为15．