题目内容
12.设随即变量X服从标准正态分布,已知P(X≤1.88)=0.97,则P(|X|≤1.88)=( )| A. | 0.94 | B. | 0.97 | C. | 0.06 | D. | 0.03 |
分析 根据所给的变量符合正态分布,根据条件中用φ(x)表示标准正态总体在区间(-∞,x)内取值的概率,对于所给的概率的式子进行整理,根据正态曲线关于x=0对称,得到要求的概率.
解答 解:∵标准正态曲线关于x=0对称,
∴P(X≥1.88)+P(X-1.88)=0.03+0.03=0.06
∴P(|X|≤1.88)=1-0.06=0.94
故选:A.
点评 本题考查正态分布曲线的特点及曲线所表示的意义,本题解题的关键是对于正态曲线的对称性的应用,本题是一个基础题.

练习册系列答案
相关题目
10.记数列{an}的前n项和为Sn,且Sn=$\int_0^n$(2ax+b)dx(a,b常数).若不等式an2+$\frac{{S_{n}^2}}{{n{^2}}}$≥ma12对任意的数列{an}及任意正整数n都成立,则实数m的取值范围为( )
| A. | $(-∞,\frac{1}{2}]$ | B. | $[{\frac{1}{5},\frac{1}{2}}]$ | C. | $[{\frac{1}{5},+∞})$ | D. | $(-∞,\frac{1}{5}]$ |
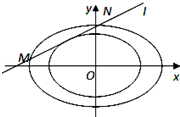 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,点M在椭圆C上,点M到椭圆C的两个焦点的距离之和是4.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,点M在椭圆C上,点M到椭圆C的两个焦点的距离之和是4.