题目内容
13.已知圆C的方程为(x+2)2+y2=4,点M在圆C上运动,点N的坐标是(2,0).(1)若线段MN的中点形成的轨迹为G,求轨迹G的方程;
(2)点P在直线x=8上,过P点引轨迹G的两条切线PA、PB,切点为A、B,求证:直线AB恒过定点.
分析 (1)设出线段MN的中点,利用中点坐标公式求出M的坐标,根据M在圆上,得到轨迹方程.
(2)由PA,PB为圆O的两条切线,根据切线的性质得到OA与AP垂直,OB与PB垂直,求出以OP为直径的圆方程,整理后,由AB为两圆的公共弦,两圆方程相减消去平方项,得到弦AB所在直线的方程,可得出此直线方程过定点.
解答 解:(1)设线段MN的中点(x,y),则M(2x-2,2y)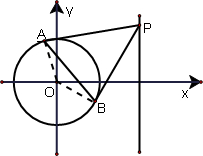
∵NM在圆(x+2)2+y2=4上运动
∴(2x-2+2)2+(2y)2=4
即x2+y2=1①;
(2)连接OA,OB,
∵PA,PB是圆C的两条切线,
∴OA⊥AP,OB⊥BP,
∴A,B在以OP为直径的圆上,
设点P的坐标为(8,b),b∈R,
则线段OP的中点坐标为(4,$\frac{b}{2}$)
∴以OP为直径的圆方程化简得:x2+y2-8x-by=0,b∈R,②
∵AB为两圆的公共弦,
∴①-②得:直线AB的方程为8x+by=1,b∈R,即8(x-$\frac{1}{8}$)+by=0,
则直线AB恒过定点($\frac{1}{8}$,0).
点评 本题考查中点的坐标公式、求轨迹方程的方法,考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,切线的性质,圆周角定理,线段中点坐标公式,两点间的距离公式,点到直线的距离公式,两圆公共弦的性质,以及恒过定点的直线方程.

练习册系列答案
相关题目
19.已知命题p:?x∈R,ex>0命题q:?x∈R,x-2>x2,则( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(?q)是真命题 | D. | 命题p∨(?q)是假命题 |
5.复数z=$\frac{3+i}{1-i}$(i为虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.从平行六面体的8个顶点中任取5个顶点为顶点,恰好构成四棱锥的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
 如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.
如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.