题目内容
4. 如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.
如图所示,椭圆C的离心率为$\frac{\sqrt{3}}{2}$,以坐标原点O为圆心,椭圆C的短半轴长为半径的圆与直线y=$\sqrt{3}$x+2相切.(1)求椭圆C的方程;
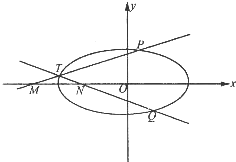
(2)设P,Q,T为椭圆C上不同的三点,且P,Q两点关于x轴对称,若直线PT,QT分别与x轴交于点M.N.求证:|OM|•|ON|为定值.
分析 (1)通过题意可知椭圆短半轴长为原点到直线y=$\sqrt{3}$x+2的距离,利用e=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{3}}{2}$,计算即得结论;
(2)通过设P(t,$\frac{\sqrt{4-{t}^{2}}}{2}$),Q(t,-$\frac{\sqrt{4-{t}^{2}}}{2}$),M(m,0),N(n,0),联立PM、NQ方程可得点T坐标,代入椭圆C方程,计算即可.
解答 (1)解:∵原点到直线y=$\sqrt{3}$x+2的距离d=$\frac{|0-0+2|}{\sqrt{(\sqrt{3})^{2}+(-1)^{2}}}$1,
∴椭圆C的短半轴长b=1,
又∵e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{3}}{2}$,∴a=2,
∴椭圆C的方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)证明:由题可设P(t,$\frac{\sqrt{4-{t}^{2}}}{2}$),Q(t,-$\frac{\sqrt{4-{t}^{2}}}{2}$),M(m,0),N(n,0),
则直线PM的方程为:y=$\frac{\sqrt{4-{t}^{2}}}{2(t-m)}$(x-m),
直线NQ的方程为:y=-$\frac{\sqrt{4-{t}^{2}}}{2(t-n)}$(x-n),
联立PM、NQ方程可得:T($\frac{(m+n)t-2mn}{2t-(m+n)}$,$\frac{1}{2}$•$\frac{(n-m)\sqrt{4-{t}^{2}}}{2t-(m+n)}$),
∵点T在椭圆C上,
∴[$\frac{(m+n)t-2mn}{2t-(m+n)}$]2+4[$\frac{1}{2}$•$\frac{(n-m)\sqrt{4-{t}^{2}}}{2t-(m+n)}$]2=4,
化简得:(4-mn)[t2-4(m+n)t+4mn]=0,
∴只需4-mn=0,即mn=4,
即|OM|•|ON|为定值.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

| A. | k>-$\frac{b}{a}$ | B. | k<$\frac{b}{a}$ | C. | k>$\frac{b}{a}$或k<-$\frac{b}{a}$ | D. | -$\frac{b}{a}$<k<$\frac{b}{a}$ |
| A. | [-1,5] | B. | [-2,2] | C. | [-2,5] | D. | [-1,2] |
| A. | 命题“若x=y,则sinx=siny”的否命题为真命题 | |
| B. | “直线x-ay=0与直线x+ay=0互相垂直”的充分条件是“a=1” | |
| C. | 命题“?x∈R,x2+x+1<0”的否定是“?x∈R,x2+x+1>0” | |
| D. | 命题:若x2=1,则x=1或x=-1的逆否命题为:若x≠1或x≠-1,则x2≠1 |
 如图,在三棱锥P-ABC中,AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E、F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
如图,在三棱锥P-ABC中,AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E、F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.