题目内容
8.椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1,过F2作直线交抛物线y2=2x于A、B两点,射线OA,OB分别交椭圆C1于点D、E,证明:$\frac{|OD||OE|}{|DE|}$为定值.分析 设直线方程为x=my+2,带入抛物线方程为y2=2x,得y2--2my-4=0,联立,根据条件列式,得出原点到直线DE的距离d=$\frac{|λ|}{\sqrt{1+{t}^{2}}}$=$\frac{\sqrt{6}}{2}$为定值,求解即可.
解答 证明:设过椭圆得F2(2,0)得直线方程为x=my+2,带入抛物线方程为y2=2x,得y2-2my-4=0.
设A(x1,y1)B(x2,y2),则y1+y2=2m,y1y2=-4
∴x1x2+y1y2=(my1+2)(my2+2)+y1y2=(1+m2)y1y2+2m(y1+y2)+4=0
∴OA⊥OB
设D(x3,y3)、E(x4,y4),直线DE的方程为x=ty+λ,代入$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1得
(t2+3)y2+2tλy+λ2-6=0,于是y3+y4=-$\frac{2tλ}{{t}^{2}+3}$,y3y4=$\frac{{λ}^{2}-6}{{t}^{2}+3}$,
从而x3x4=$\frac{3{λ}^{2}-6{t}^{2}}{{t}^{2}+3}$,
∵OA⊥OB,∴OD⊥OE,∴x3x4+y3y4=0,
代入整理得2λ2=3(t2+1),过原点O作直线DE的垂线OM,垂足为M,
∴原点到直线DE的距离d=$\frac{|λ|}{\sqrt{1+{t}^{2}}}$=$\frac{\sqrt{6}}{2}$为定值,
∵△DOE为直角三角形,∴$\frac{1}{2}|OD||OE|=\frac{1}{2}|DE|d$,∴$\frac{|OD||OE|}{|DE|}$=$\frac{\sqrt{6}}{2}$为定值.
点评 本题主要考查了直线与圆锥曲线的综合应用,考查直线与抛物线的位置关系,考查学生分析解决问题的能力,属于中档题.

| A. | (11,12) | B. | (12,13) | C. | (13,14) | D. | (13,12) |
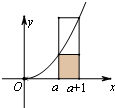 如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即a2<${∫}_{a}^{a+1}$x2dx<(a+1)2.类比之,?n∈N*,$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )
如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即a2<${∫}_{a}^{a+1}$x2dx<(a+1)2.类比之,?n∈N*,$\frac{1}{n+1}$+$\frac{1}{n+2}$+…+$\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | ln2 | D. | ln$\frac{5}{2}$ |
| A. | {-2,1,3} | B. | {-2,1,2} | C. | {-2,1} | D. | {-2,1,5} |
 如图,在三棱锥P-ABC中,AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E、F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
如图,在三棱锥P-ABC中,AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E、F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.