题目内容
7.(Ⅰ)已知正数a1、a2满足a1+a2=1,求证:a1log2a1+a2log2a2≥-1;(Ⅱ)若正数a1、a2、a3、a4满足a1+a2+a3+a4=1,求证:a1log2a1+a2log2a2+a3log2a3+a4log2a4≥-2.
分析 (Ⅰ)先求函数f(x)=xlog2x+(1-x)log2(1-x)(x∈(0,1))的最小值.得出a1,a2的大小关系,即可证明.
(Ⅱ)由(Ⅰ)的结论可推知:$\frac{a_1}{x}{log_2}\frac{a_1}{x}+\frac{a_2}{x}{log_2}\frac{a_2}{x}≥-1$,整理式子,利用此式即可得到证明.
解答 解:(Ⅰ)证明:先求函数f(x)=xlog2x+(1-x)log2(1-x)(x∈(0,1))的最小值
∵f'(x)=(xlog2x)'+[(1-x)log2(1-x)]'=${log_2}x-{log_2}(1-x)+\frac{1}{ln2}-\frac{1}{ln2}$=log2x-log2(1-x)于是$f'({\frac{1}{2}})=0$,
当0<$x<\frac{1}{2}$时,f'(x)=log2x-log2(1-x)<0,f(x)在区间$({0,\frac{1}{2}})$是减函数,
当$\frac{1}{2}<x<1$时,f'(x)=log2x-log2(1-x)>0,f(x)在区间$({\frac{1}{2},1})$是增函数,
所以$f(x)在x=\frac{1}{2}$时取得最小值,$f({\frac{1}{2}})=-1$,∴f(x)≥-1
∵a1>0,a2>0,a1+a2=1,∴a2=1-a1,由①得
∴a1log2a1+a2log2a=a1log2a1+(1-a1)log2(1-a2)≥-1
(Ⅱ)证明:∵a1+a2+a3+a4=1,设a1+a2=1-(a3+a4)=x
则$\frac{a_1}{x}+\frac{a_2}{x}=1$,由(Ⅰ)的结论可得:$\frac{a_1}{x}{log_2}\frac{a_1}{x}+\frac{a_2}{x}{log_2}\frac{a_2}{x}≥-1$?a1log2a1+a2log2a2-(a1+a2)log2x≥-x?a1log2a1+a2log2a2≥-x+xlog2x…①
同理∵a3+a4=1-x有:a3log2a3+a4log2a4≥-(1-x)+(1-x)log2(1-x)…②
①+②得:a1log2a1+a2log2a2+a3log2a3+a4log2a4≥-1+xlog2x+(1-x)log2(1-x)
由于f(x)=xlog2x+(1-x)log2x≥-1
∴a1log2a1+a2log2a2+a3log2a3+a4log2a4≥-2
点评 本题主要考查导数在证明不等式中的应用,属于中档题型,高考中时有涉及.

| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
| A. | 恰有一个最小周期为1的周期点,恰有一个最小周期为2的周期点 | |
| B. | 恰有一个最小周期为1的周期点,恰有两个最小周期为2的周期点 | |
| C. | 恰有两个最小周期为1的周期点,恰有两个最小周期为2的周期点 | |
| D. | 恰有两个最小周期为1的周期点,恰有四个最小周期为2的周期点 |
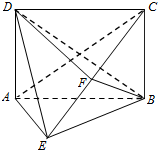 如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,
如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,