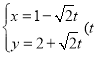题目内容
【题目】设甲、乙两位同学上学期间，每天7：30之前到校的概率均为
.假定甲、乙两位同学到校情况互不影响，且任一同学每天到校情况相互独立.
（Ⅰ）用
表示甲同学上学期间的三天中7：30之前到校的天数，求随机变量的分布列和数学期望；
（Ⅱ）设
为事件“上学期间的三天中，甲同学在7：30之前到校的天数比乙同学在7：30之前到校的天数恰好多2”，求事件发生的概率.
【答案】（Ⅰ）见解析；（Ⅱ）
【解析】
(Ⅰ)由题意可知分布列为二项分布，结合二项分布的公式求得概率可得分布列，然后利用二项分布的期望公式求解数学期望即可；
(Ⅱ)由题意结合独立事件概率公式计算可得满足题意的概率值.
(Ⅰ)因为甲同学上学期间的三天中到校情况相互独立，且每天7:30之前到校的概率均为
，
故
，从面
.
所以，随机变量
的分布列为：
| 0 | 1 | 2 | 3 |
|
|
|
|
|
随机变量的数学期望
.
(Ⅱ)设乙同学上学期间的三天中7:30之前到校的天数为
，则
.
且
.
由题意知事件
与
互斥，
且事件
与
，事件
与
均相互独立，
从而由(Ⅰ)知：
.
练习册系列答案
相关题目
【题目】随着科技的发展，网购已经逐渐融入了人们的生活.在家里面不用出门就可以买到自己想要的东西，在网上付款即可，两三天就会送到自己的家门口，如果近的话当天买当天就能送到，或者第二天就能送到，所以网购是非常方便的购物方式.某公司组织统计了近五年来该公司网购的人数
（单位：人）与时间
（单位：年）的数据，列表如下：
| 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
（1）依据表中给出的数据，是否可用线性回归模型拟合
与
的关系，请计算相关系数
并加以说明（计算结果精确到0.01）.（若
，则线性相关程度很高，可用线性回归模型拟合）
附：相关系数公式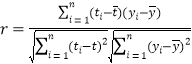
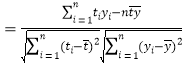，参考数据
.
（2）建立关于的回归方程，并预测第六年该公司的网购人数（计算结果精确到整数）.
（参考公式：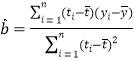
，
）
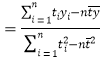