题目内容
若椭圆长轴长与短轴长之比为2,它的一个焦点是(2 ,0),则椭圆的标准方程是
,0),则椭圆的标准方程是
 ,0),则椭圆的标准方程是
,0),则椭圆的标准方程是 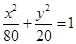
试题分析:由题意
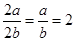 ,c=2
,c=2 ,∴
,∴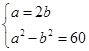 ,∴
,∴ ,∴所求椭圆的标准方程为
,∴所求椭圆的标准方程为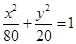
点评:弄清椭圆中a,b,c中的关系是用待定系数法的关键,解题时注意讨论焦点的位置

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
题目内容
 ,0),则椭圆的标准方程是
,0),则椭圆的标准方程是 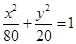
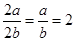 ,c=2
,c=2 ,∴
,∴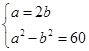 ,∴
,∴ ,∴所求椭圆的标准方程为
,∴所求椭圆的标准方程为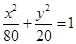

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案