题目内容
已知椭圆的两个焦点分别为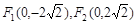 ,离心率
,离心率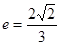 。
。
(1)求椭圆方程;
(2)一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N,且线段MN中点的横坐标为–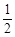 ,求直线l倾斜角的取值范围。
,求直线l倾斜角的取值范围。
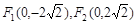 ,离心率
,离心率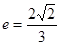 。
。(1)求椭圆方程;
(2)一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N,且线段MN中点的横坐标为–
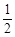 ,求直线l倾斜角的取值范围。
,求直线l倾斜角的取值范围。(Ⅰ)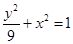 ;(Ⅱ)
;(Ⅱ)
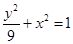 ;(Ⅱ)
;(Ⅱ)
试题分析:(Ⅰ)设椭圆方程为

由已知,
 ,由
,由 解得a=3,
解得a=3,
∴
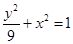 为所求
为所求 (Ⅱ)解法一:设直线l的方程为y=kx+b(k≠0)
解方程组
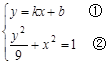
将①代入②并化简,得


将④代入③化简后,得
 。
。 解得
 ∴
∴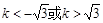 , 所以倾斜角
, 所以倾斜角 。
。 解法二:(点差法)设
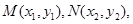
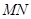 的中点为
的中点为 在椭圆
在椭圆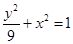 内,且直线l不与坐标轴平行。
内,且直线l不与坐标轴平行。因此,
 ,
,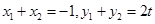
∵
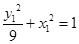 ,
,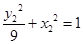
∴两式相减得

即
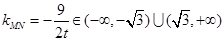
∴
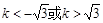 。所以倾斜角
。所以倾斜角
点评:典型题,涉及直线与椭圆的位置关系问题,通过联立方程组得到一元二次方程,应用韦达定理可实现整体代换,简化解题过程。涉及椭圆上两点问题,可以利用“点差法”,建立连线的斜率与a,b的关系。

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 ,右焦点
,右焦点 ,双曲线的实轴为
,双曲线的实轴为 ,
, 为双曲线上一点(不同于
为双曲线上一点(不同于 ),直线
),直线 ,
, 分别与直线
分别与直线 交于
交于 两点
两点 是否为定值,若为定值,求出该值;若不为定值,说明理由。
是否为定值,若为定值,求出该值;若不为定值,说明理由。 与直线4x+3y + 1 =0相切,动圆M与
与直线4x+3y + 1 =0相切,动圆M与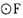 及y轴都相切. (I )求点M的轨迹C的方程;(II)过点F任作直线l,交曲线C于A,B两点,由点A,B分别向
及y轴都相切. (I )求点M的轨迹C的方程;(II)过点F任作直线l,交曲线C于A,B两点,由点A,B分别向 各引一条切线,切点 分别为P,Q,记
各引一条切线,切点 分别为P,Q,记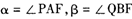 .求证
.求证 是定值.
是定值.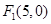 ,
,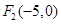 ,曲线上的点P到
,曲线上的点P到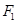 、
、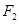 的距离之差的绝对值是6,则该曲线的方程为( )
的距离之差的绝对值是6,则该曲线的方程为( )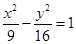
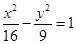
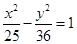
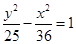
 ,0),则椭圆的标准方程是
,0),则椭圆的标准方程是  (a>0,b>0)的两个焦点为
(a>0,b>0)的两个焦点为 ,若P为其上一点,
,若P为其上一点,  , 则双曲线离心率的取值范围为( )
, 则双曲线离心率的取值范围为( ) )
)

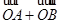 与
与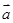 =(3,-1)共线.
=(3,-1)共线.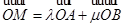 (
(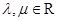 ),证明
),证明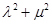 为定值.
为定值. 分别是双曲线
分别是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若
两点,若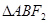 是钝角三角形,则该双曲线离心率的取值范围是
是钝角三角形,则该双曲线离心率的取值范围是

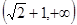

 与直线
与直线 交于
交于 点.
点. 过
过 垂直时,求直线
垂直时,求直线 到直线
到直线 时,求直线
时,求直线