题目内容
如果方程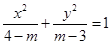 表示焦点在
表示焦点在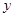 轴上的椭圆,则
轴上的椭圆,则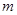 的取值范围是
的取值范围是
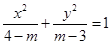 表示焦点在
表示焦点在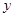 轴上的椭圆,则
轴上的椭圆,则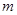 的取值范围是
的取值范围是A.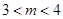 | B.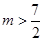 | C. | D.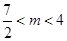 |
D
试题分析:因为方程
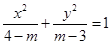 表示焦点在
表示焦点在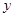 轴上的椭圆,所以
轴上的椭圆,所以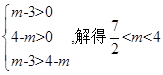 。
。点评:熟练掌握判断椭圆、双曲线以及圆的方程的特点。方程
 ,当
,当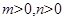 且
且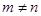 时表示椭圆;(当
时表示椭圆;(当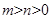 时,表示焦点在x轴上的椭圆;当
时,表示焦点在x轴上的椭圆;当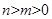 时表示焦点在y轴上的椭圆。)当
时表示焦点在y轴上的椭圆。)当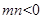 时,表示双曲线;当
时,表示双曲线;当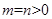 时,表示圆。
时,表示圆。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
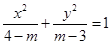 表示焦点在
表示焦点在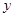 轴上的椭圆,则
轴上的椭圆,则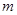 的取值范围是
的取值范围是A.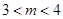 | B.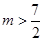 | C. | D.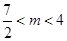 |
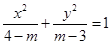 表示焦点在
表示焦点在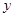 轴上的椭圆,所以
轴上的椭圆,所以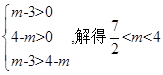 。
。 ,当
,当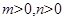 且
且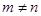 时表示椭圆;(当
时表示椭圆;(当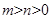 时,表示焦点在x轴上的椭圆;当
时,表示焦点在x轴上的椭圆;当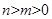 时表示焦点在y轴上的椭圆。)当
时表示焦点在y轴上的椭圆。)当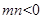 时,表示双曲线;当
时,表示双曲线;当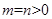 时,表示圆。
时,表示圆。
 名校课堂系列答案
名校课堂系列答案