题目内容
已知⊙O: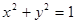 ,
,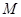 为抛物线
为抛物线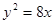 的焦点,
的焦点,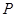 为⊙O外一点,由
为⊙O外一点,由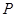 作⊙O的切线与圆相切于
作⊙O的切线与圆相切于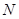 点,且
点,且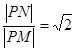
(1)求点P的轨迹C的方程
(2)设A为抛物线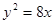 准线上任意一点,由A向曲线C作两条切线AB、AC,其中B、C为切点.求证:直线BC必过定点
准线上任意一点,由A向曲线C作两条切线AB、AC,其中B、C为切点.求证:直线BC必过定点
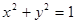 ,
,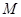 为抛物线
为抛物线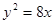 的焦点,
的焦点,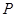 为⊙O外一点,由
为⊙O外一点,由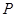 作⊙O的切线与圆相切于
作⊙O的切线与圆相切于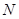 点,且
点,且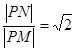
(1)求点P的轨迹C的方程
(2)设A为抛物线
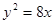 准线上任意一点,由A向曲线C作两条切线AB、AC,其中B、C为切点.求证:直线BC必过定点
准线上任意一点,由A向曲线C作两条切线AB、AC,其中B、C为切点.求证:直线BC必过定点(1) (2)见解析
(2)见解析
 (2)见解析
(2)见解析(1)先求出抛物线的焦点M(2,0),设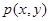 ,因为
,因为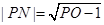 ,
,
然后根据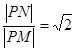 坐标化建立方程,化简可得点P的轨迹方程.
坐标化建立方程,化简可得点P的轨迹方程.
(2)抛物线的准线为x=-2,设A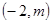
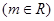 ,再根据
,再根据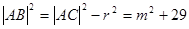 ,
,
可得以A为圆心,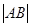 为半径的圆的方程为
为半径的圆的方程为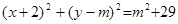 ,再与圆O的方程作差可得公共弦所在直线方程,从而可找到直线所过定点.
,再与圆O的方程作差可得公共弦所在直线方程,从而可找到直线所过定点.
解:(1)抛物线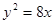 的焦点M(2,0)………….1分 设
的焦点M(2,0)………….1分 设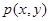
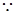
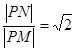
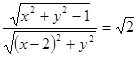 ………4分 化简得方程
………4分 化简得方程
 P点轨迹为⊙C:
P点轨迹为⊙C:  …………6分
…………6分
(2)抛物线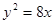 准线方程为
准线方程为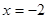 …………..7分 设A
…………..7分 设A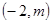
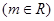
⊙C: 化为
化为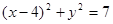 ……….. ①
……….. ①
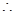 C(4,0),半径
C(4,0),半径 …………..8分 由已知得
…………..8分 由已知得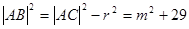
以A为圆心,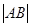 为半径的圆的方程为
为半径的圆的方程为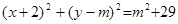
即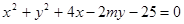 ………..②……………10分
………..②……………10分
由于BC为两圆公共弦所在直线 由②-①得BC直线方程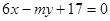 …………12分
…………12分
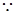
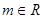
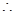
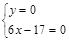 得
得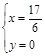
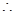 直线BC过定点
直线BC过定点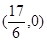 …………14分
…………14分
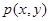 ,因为
,因为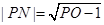 ,
,然后根据
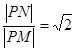 坐标化建立方程,化简可得点P的轨迹方程.
坐标化建立方程,化简可得点P的轨迹方程.(2)抛物线的准线为x=-2,设A
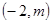
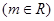 ,再根据
,再根据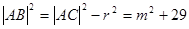 ,
,可得以A为圆心,
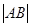 为半径的圆的方程为
为半径的圆的方程为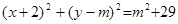 ,再与圆O的方程作差可得公共弦所在直线方程,从而可找到直线所过定点.
,再与圆O的方程作差可得公共弦所在直线方程,从而可找到直线所过定点.解:(1)抛物线
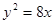 的焦点M(2,0)………….1分 设
的焦点M(2,0)………….1分 设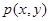
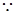
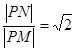
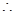
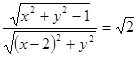 ………4分 化简得方程
………4分 化简得方程
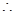 P点轨迹为⊙C:
P点轨迹为⊙C:  …………6分
…………6分(2)抛物线
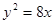 准线方程为
准线方程为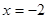 …………..7分 设A
…………..7分 设A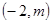
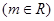
⊙C:
 化为
化为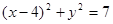 ……….. ①
……….. ①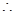 C(4,0),半径
C(4,0),半径 …………..8分 由已知得
…………..8分 由已知得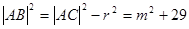
以A为圆心,
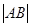 为半径的圆的方程为
为半径的圆的方程为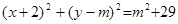
即
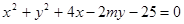 ………..②……………10分
………..②……………10分由于BC为两圆公共弦所在直线 由②-①得BC直线方程
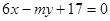 …………12分
…………12分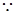
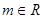
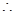
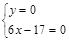 得
得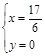
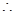 直线BC过定点
直线BC过定点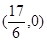 …………14分
…………14分
练习册系列答案
相关题目
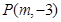 到焦点的距离等于5,
到焦点的距离等于5,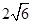
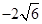

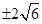
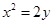 的焦点到准线的距离为( )
的焦点到准线的距离为( )
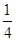
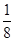
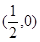 的距离与P到直线
的距离与P到直线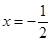 距离相等
距离相等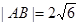 ,求直线l的方程;
,求直线l的方程;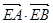 恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由. 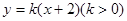 与抛物线
与抛物线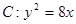 相交于A,B两点,F为C的焦点,若|FA|=2|FB|,则实数k的值为 ( )
相交于A,B两点,F为C的焦点,若|FA|=2|FB|,则实数k的值为 ( )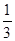
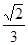
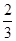
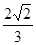
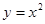 上的点M(
上的点M(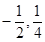 )的切线的倾斜角为( )
)的切线的倾斜角为( )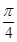
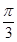

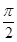
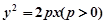 ,过其焦点且斜率为1的
,过其焦点且斜率为1的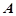 、
、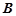 两点,若线段
两点,若线段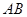 的中点的纵
的中点的纵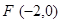 ,求它的标准方程 ;
,求它的标准方程 ;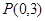 ,求椭圆的标准方程;
,求椭圆的标准方程;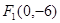 ,
,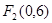 ,双曲线上一点
,双曲线上一点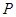 到
到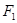 ,
,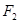 的距离差的绝对值等于8, 求双曲线的方程.
的距离差的绝对值等于8, 求双曲线的方程.