题目内容
.已知直线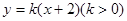
与抛物线
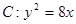相交于A，B两点，F为C的焦点，若|FA|=2|FB|，则实数k的值为 （ ）
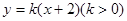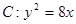与抛物线相交于A，B两点，F为C的焦点，若|FA|=2|FB|，则实数k的值为 （ ）A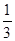． | B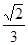． | C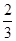． | D． |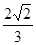
D
解：设抛物线C：y2=8x的准线为l：x=-2
直线y=k（x+2）（k＞0）恒过定点P（-2，0）
如图过A、B分别作AM⊥l于M，BN⊥l于N，
由|FA|=2|FB|，则|AM|=2|BN|，
点B为AP的中点、连接OB，
则|OB|=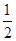
|AF|，
∴|OB|=|BF|，点B的横坐标为1，
故点B的坐标为(1，2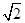
)∴k=，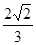
故选D
直线y=k（x+2）（k＞0）恒过定点P（-2，0）
如图过A、B分别作AM⊥l于M，BN⊥l于N，
由|FA|=2|FB|，则|AM|=2|BN|，
点B为AP的中点、连接OB，
则|OB|=
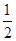|AF|，∴|OB|=|BF|，点B的横坐标为1，
故点B的坐标为(1，2
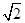)∴k=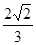，故选D
练习册系列答案
相关题目
，
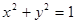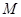为抛物线
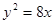的焦点，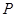
为⊙O外一点，由
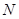点，且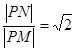
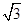，且其三个顶点均在抛物线E：x2＝2py(p＞0)上.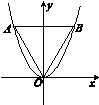
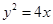的焦点F，直线l过点
。
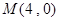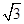，求直线l的斜率；
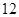点时，拱顶离水面
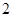米，桥下的水面宽
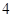米；下午
米，桥下的水面宽 米.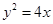
的焦点
的直线交抛物线于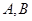
两点，点
是原点，若
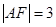，则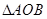
的面积为（ ）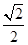
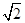
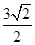
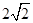
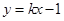与抛物线C：
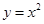，相交于两点
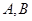，设点
，
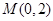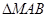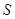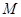的面积为
.
连线距离为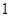
的点至多存在一个，求
，且满足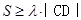
恒成立，求正数
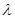的范围.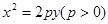 
的焦点作斜率为1的直线与该抛物线交于A、B两点，A、B在
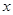轴上的正射影分别为D、C。若梯形ABCD的面积为
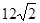，则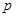
= 。
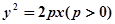的所有焦点弦中，弦长的最小值为（ ）