题目内容
若抛物线y2=-2px(p>0)上有一点M,其横坐标为-9.它到焦点的距离为10,求抛物线方程和M点的坐标.
y2=-4x,M(-9,6)或M(-9,-6)
本题考查抛物线的几何性质,解题时要认真审题,注意挖掘题设中的隐含条件。
(1)(1)抛物线的开口向右,焦点在x轴的正半轴上,故可求焦点F坐标;
(2)利用点A(-2,3)到抛物线y2=2px(p>0)焦点F的距离为5,从而 利用定义故可求出抛物线的方程.
解:由抛物线定义知焦点为F(-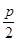 ,0),准线为x=
,0),准线为x=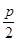 ,
,
由题意设M到准线的距离为|MN|, 则|MN|=|MF|=10, 即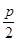 -(-9)=10,
-(-9)=10,
∴p=2.故抛物线方程为y2=-4x,将M(-9,y)代入y2=-4x,解得y=±6,
∴M(-9,6)或M(-9,-6).
(1)(1)抛物线的开口向右,焦点在x轴的正半轴上,故可求焦点F坐标;
(2)利用点A(-2,3)到抛物线y2=2px(p>0)焦点F的距离为5,从而 利用定义故可求出抛物线的方程.
解:由抛物线定义知焦点为F(-
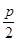 ,0),准线为x=
,0),准线为x=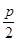 ,
,由题意设M到准线的距离为|MN|, 则|MN|=|MF|=10, 即
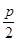 -(-9)=10,
-(-9)=10,∴p=2.故抛物线方程为y2=-4x,将M(-9,y)代入y2=-4x,解得y=±6,
∴M(-9,6)或M(-9,-6).

练习册系列答案
相关题目

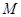 的坐标为
的坐标为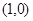 ;
;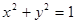 ,
,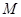 为抛物线
为抛物线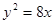 的焦点,
的焦点,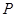 为⊙O外一点,由
为⊙O外一点,由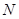 点,且
点,且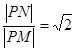
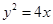 的焦点F,直线l过点
的焦点F,直线l过点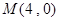 。
。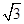 ,求直线l的斜率;
,求直线l的斜率;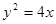 及点
及点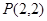 ,直线
,直线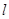 的斜率为1且不过点P,与抛物线交于A,B两点。
的斜率为1且不过点P,与抛物线交于A,B两点。 轴上截距的取值范围;
轴上截距的取值范围;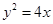 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于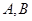 两点,点
两点,点 是原点,若
是原点,若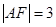 ,则
,则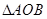 的面积为( )
的面积为( )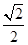
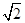
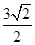
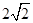
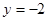 上有一个动点
上有一个动点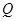 ,过点
,过点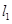 垂直于
垂直于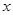 轴,动点
轴,动点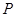 在
在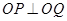 (
(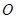 为坐标原点),记点
为坐标原点),记点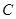 .
. 是曲线
是曲线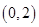 到直线
到直线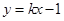 与抛物线C:
与抛物线C: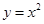 ,相交于两点
,相交于两点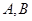 ,设点
,设点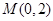 ,
,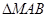 的面积为
的面积为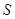 .
.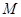 连线距离为
连线距离为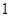 的点至多存在一个,求
的点至多存在一个,求 ,且满足
,且满足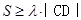 恒成立,求正数
恒成立,求正数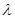 的范围.
的范围. 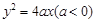 的焦点坐标是( )
的焦点坐标是( )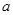 , 0)
, 0)