题目内容
1.已知函数f(x)=ax3+x2f′(1)+1,且f′(-1)=9.(1)求曲线f(x)在x=1处的切线方程;
(2)若存在x∈(1,+∞)使得函数f(x)<m成立,求实数m的取值范围.
分析 (1)求出函数的导数,令x=1,x=-1,得到方程,解得a=1,求得切线的斜率和切点,由点斜式方程可得切线方程;
(2)存在x∈(1,+∞)使得函数f(x)<m成立,即有m>f(x)min,求出函数f(x)在(1,+∞)的单调区间,求得最小值即可.
解答 解:(1)函数f(x)=ax3+x2f′(1)+1的导数
f′(x)=3ax2+2xf′(1),
令x=1,则f′(1)=3a+2f′(1),即为f′(1)=-3a,
由f′(-1)=9,可得3a-2•(-3a)=9,
解得a=1,即有f′(1)=-3,
则f(x)=x3-3x2+1,
即有f(1)=1-3+1=-1,
则f(x)在x=1处的切线方程为y+1=-3(x-1),
即有3x+y-2=0;
(2)f(x)=x3-3x2+1的导数f′(x)=3x2-6x,
当1<x<2时,f′(x)<0,f(x)递减;
当x>2时,f′(x)>0,f(x)递增.
即有x=2处,f(x)取得极小值,且为最小值,且f(2)=-3,
存在x∈(1,+∞)使得函数f(x)<m成立,
即有m>f(x)min=-3,
故m的取值范围为(-3,+∞).
点评 本题考查导数的运用:求切线方程和单调区间、极值和最值,同时考查不等式存在性问题,注意转化为求函数的最值问题,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
12.若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$i | C. | $\frac{4}{5}$i | D. | 4 |
13.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上是减函数,若$f({ln\frac{n}{m}})-f(1)>0$,则$\frac{{{m^2}+{n^2}}}{mn}$的取值范围是( )
| A. | [2,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
10.i为虚数单位,(1+i)$\overline{z}$=(1-i)2,则|z|=( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
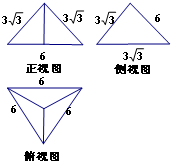 正四面体(即各条棱长均相等的三棱锥)的棱长为6,某学生画出该正四面体的三视图如下,其中有一个视图是错误的,则该视图修改正确后对应图形的面积为6$\sqrt{6}$.该正四面体的体积为18$\sqrt{2}$.
正四面体(即各条棱长均相等的三棱锥)的棱长为6,某学生画出该正四面体的三视图如下,其中有一个视图是错误的,则该视图修改正确后对应图形的面积为6$\sqrt{6}$.该正四面体的体积为18$\sqrt{2}$.