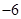题目内容
若存在过点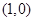 的直线与曲线
的直线与曲线 和
和 都相切,求
都相切,求 的值
的值
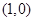 的直线与曲线
的直线与曲线 和
和 都相切,求
都相切,求 的值
的值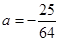 或
或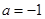 .
.试题分析:已知点
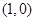 不知曲线
不知曲线 上,容易求出过点
上,容易求出过点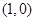 的直线与曲线
的直线与曲线 相切的切点的坐标,进而求出切线所在的方程;再利用切线与
相切的切点的坐标,进而求出切线所在的方程;再利用切线与 相切,只有一个公共点,两个方程联系,得到二元一次方程,利用判别式为、,解出
相切,只有一个公共点,两个方程联系,得到二元一次方程,利用判别式为、,解出 的值.
的值.试题解析:设过
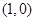 的直线与
的直线与 相切于点
相切于点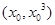 ,所以切线方程为
,所以切线方程为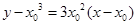 ,
,即
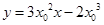 ,又
,又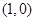 在切线上,则
在切线上,则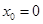 或
或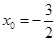 ,
,当
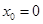 时,由
时,由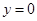 与
与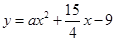 相切可得
相切可得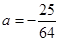 ,
,当
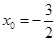 时,由
时,由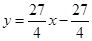 与
与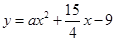 相切可得
相切可得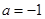 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
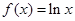 ,
,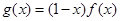
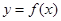 在点(1,0)处的切线方程;
在点(1,0)处的切线方程; 及
及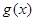 在区间
在区间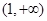 上的单调性;
上的单调性; 在
在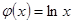
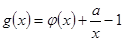 在点
在点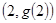 处的切线与直线
处的切线与直线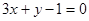 平行,求
平行,求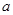 的值;
的值;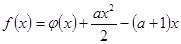 ,
, ,且
,且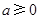 .求函数
.求函数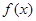 的单调递增区间.
的单调递增区间. 的前
的前 项和为
项和为 ,且
,且 ,对任意
,对任意 ,都有
,都有
 .
.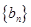 满足
满足 ,求数列
,求数列 .
.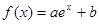 在
在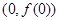 处切线为
处切线为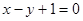 .
.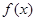 的解析式;
的解析式;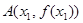 ,
,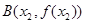 ,
,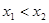 ,
,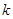 表示直线
表示直线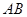 的斜率,求证:
的斜率,求证: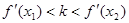 .
. 的导数
的导数 ,则数列
,则数列 的前n项和( )
的前n项和( )



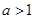 ,且函数
,且函数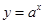 与函数
与函数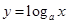 的图象有且仅有一个公共点,则此公共点的坐标为 .
的图象有且仅有一个公共点,则此公共点的坐标为 . ,且f(x)的图象在x=1处与直线y=2相切.
,且f(x)的图象在x=1处与直线y=2相切. ,则
,则 ( )
( )