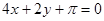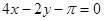题目内容
已知函数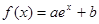 在
在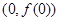 处切线为
处切线为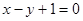 .
.
(1)求 的解析式;
的解析式;
(2)设 ,
,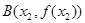 ,
,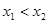 ,
, 表示直线
表示直线 的斜率,求证:
的斜率,求证: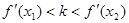 .
.
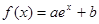 在
在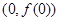 处切线为
处切线为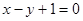 .
.(1)求
 的解析式;
的解析式;(2)设
 ,
,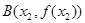 ,
,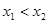 ,
, 表示直线
表示直线 的斜率,求证:
的斜率,求证: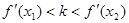 .
.(1)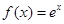 ;(2)见解析
;(2)见解析
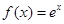 ;(2)见解析
;(2)见解析试题分析:(1)将切点代入切线方程可得
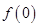 。由切线方程可知切线的斜率为1,根据导数的几何意义可得
。由切线方程可知切线的斜率为1,根据导数的几何意义可得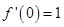 。解方程组即可求得
。解方程组即可求得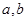 的值。从而可得
的值。从而可得 的解析式。(2)可将问题转化证
的解析式。(2)可将问题转化证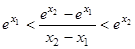 ,因为
,因为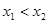 所以即证
所以即证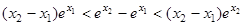 ,分别去证
,分别去证 和
和 。再证这两个不等式时均采用构造函数求其最值的方法证明即可。用其他方法证明也可。
。再证这两个不等式时均采用构造函数求其最值的方法证明即可。用其他方法证明也可。试题解析:(1)
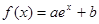 ,
,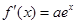 ,∴由
,∴由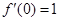 得
得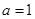 3分
3分把
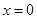 代入
代入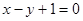 得
得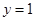 ,即
,即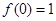 ,∴
,∴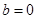
∴
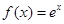 . 5分
. 5分(2)『证法1』:
证明:由(1)
 ∴证明
∴证明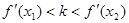 即证
即证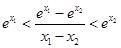
各项同除以
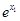 ,即证
,即证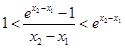 8分
8分令
 ,则
,则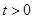 ,这样只需证明
,这样只需证明
 即
即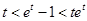
设
 ,
,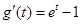 ,
,∵
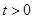 ,∴
,∴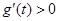 ,即
,即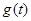 在
在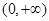 上是增函数
上是增函数∴
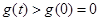 ,即
,即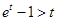 10分
10分设
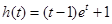 ,
,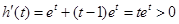
∴
 在
在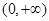 也是在增函数
也是在增函数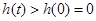 ,即
,即
从而证明了
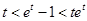 成立,所以
成立,所以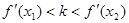 成立. 12分
成立. 12分『证法2』:
证明:
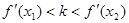 等价于
等价于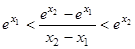
即
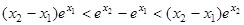 8分
8分先证
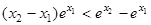 ,
,问题等价于
 ,即
,即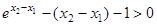
设
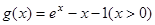 ,则
,则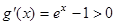
∴
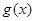 在
在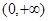 上是增函数,
上是增函数,
∵
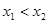 ,∴
,∴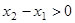 ,∴
,∴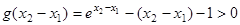 ,
,得证. 10分
再证
 ,
,问题等价于
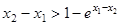 ,即
,即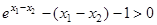
设
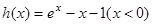 ,则
,则
∴
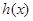 在
在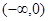 上是减函数,
上是减函数,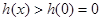
∵
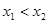 ,∴
,∴ ,∴
,∴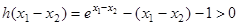 ,
,得证.综上,
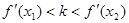 . 12分
. 12分
练习册系列答案
相关题目
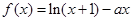 在
在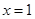 处的切线的斜率为
处的切线的斜率为 .
.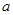 的值及函数
的值及函数 的最大值;
的最大值;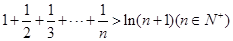 .
.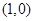 的直线与曲线
的直线与曲线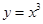 和
和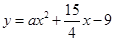 都相切,求
都相切,求 的值
的值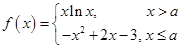 ,其中
,其中 .
. 时,求函数
时,求函数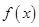 的图象在点
的图象在点 处的切线方程;
处的切线方程;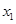 、
、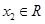 ,且
,且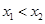 ,都有
,都有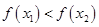 ,求
,求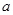 的取值范围.
的取值范围. m(x-1)2-2x+3+ln x,m≥1.
m(x-1)2-2x+3+ln x,m≥1. 时,求函数f(x)在区间[1,3]上的极小值;
时,求函数f(x)在区间[1,3]上的极小值;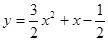 的某一切线与直线
的某一切线与直线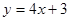 平行,则切线方程为 .
平行,则切线方程为 . ,其中
,其中 .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;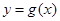 在点
在点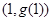 处的切线方程为
处的切线方程为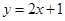 ,则曲线
,则曲线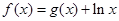 在点
在点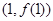 处切线的方程为 .
处切线的方程为 . 处的切线方程是
处的切线方程是