题目内容
已知函数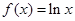 ,
,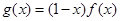
(1)求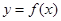 在点(1,0)处的切线方程;
在点(1,0)处的切线方程;
(2)判断 及
及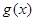 在区间
在区间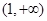 上的单调性;
上的单调性;
(3)证明: 在
在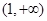 上恒成立.
上恒成立.
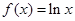 ,
,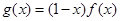
(1)求
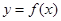 在点(1,0)处的切线方程;
在点(1,0)处的切线方程;(2)判断
 及
及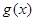 在区间
在区间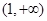 上的单调性;
上的单调性;(3)证明:
 在
在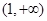 上恒成立.
上恒成立. (1)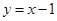 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
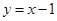 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.试题分析:(1)首先求出切线斜率即f’(x)利用点斜式即可求出答案;
(2)首先求出
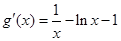 ,判断
,判断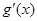 在(1,+∞)是否大于零,判断g(x)在区间
在(1,+∞)是否大于零,判断g(x)在区间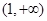 上的单调性,在求出
上的单调性,在求出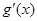 的导数判断其在(1,+∞)是否大于零,即可得到
的导数判断其在(1,+∞)是否大于零,即可得到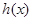 在(1,+∞)上的单调性;
在(1,+∞)上的单调性;(3)对不等式
 两边取对数,化简得
两边取对数,化简得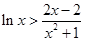 ,设函数
,设函数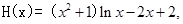
将原问题转化为则
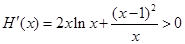 在
在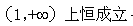 ,求出H(x)的最小值大于0 即可.
,求出H(x)的最小值大于0 即可.(1)
 1分
1分 2分
2分 3分
3分(2)
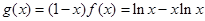
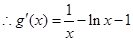 4分
4分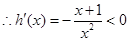 在
在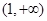 上恒成立 6分
上恒成立 6分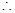
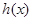 在
在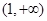 上单调递减
上单调递减 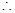
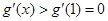
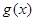 在
在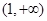 上单调递增 7分
上单调递增 7分(3)
 即
即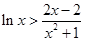 8分
8分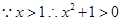
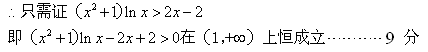
设函数
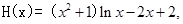
则
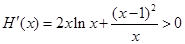 在
在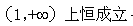
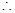
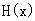 在
在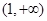 上单调递增
上单调递增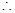
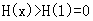 11分
11分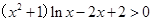 即
即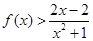 在
在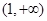 上恒成立 12分.
上恒成立 12分.
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
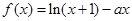 在
在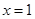 处的切线的斜率为
处的切线的斜率为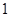 .
.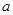 的值及函数
的值及函数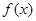 的最大值;
的最大值;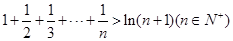 .
. 的直线与曲线
的直线与曲线 和
和 都相切,求
都相切,求 的值
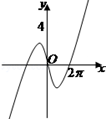
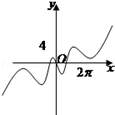
的值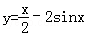 的图象大致是( )
的图象大致是( )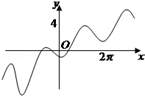
 是一个观光区的平面示意图,建立平面直角坐标系,使顶点
是一个观光区的平面示意图,建立平面直角坐标系,使顶点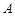 在坐标原点
在坐标原点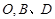 分别为
分别为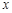 轴、
轴、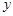 轴,
轴,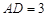 (百米),
(百米),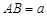 (百米)(
(百米)(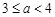 )观光区中间叶形阴影部分
)观光区中间叶形阴影部分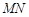 是一个人工湖,它的左下方边缘曲线是函数
是一个人工湖,它的左下方边缘曲线是函数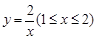 的图象的一段.为了便于游客观光,拟在观光区铺设一条穿越该观光区的直路(宽度不计),要求其与人工湖左下方边缘曲线段
的图象的一段.为了便于游客观光,拟在观光区铺设一条穿越该观光区的直路(宽度不计),要求其与人工湖左下方边缘曲线段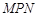 相切(切点记为
相切(切点记为 ),并把该观光区分为两部分,且直线
),并把该观光区分为两部分,且直线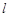 左下部分建设为花圃.记点
左下部分建设为花圃.记点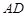 的距离为
的距离为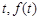 表示花圃的面积.
表示花圃的面积.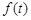 的表达式;
的表达式;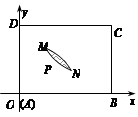
 上任意一点,则点P到直线y=x-2的最小值为( ).
上任意一点,则点P到直线y=x-2的最小值为( ).


 :
: 在点
在点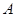 处的切线
处的切线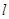 恰好经过坐标原点,则曲线
恰好经过坐标原点,则曲线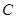 直线
直线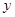 轴围成的图形面积为( )
轴围成的图形面积为( )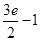
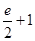
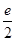
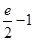
 的某一切线与直线
的某一切线与直线 平行,则切线方程为 .
平行,则切线方程为 .