题目内容
已知函数f(x)＝
，且f(x)的图象在x＝1处与直线y＝2相切．
(1)求函数f(x)的解析式；
(2)若P(x0，y0)为f(x)图象上的任意一点，直线l与f(x)的图象切于P点，求直线l的斜率k的取值范围．
，且f(x)的图象在x＝1处与直线y＝2相切．(1)求函数f(x)的解析式；
(2)若P(x0，y0)为f(x)图象上的任意一点，直线l与f(x)的图象切于P点，求直线l的斜率k的取值范围．
（1）f(x)＝
（2）k∈
（2）k∈(1)对函数f(x)求导，得f′(x)＝
.
∵f(x)的图象在x＝1处与直线y＝2相切，
∴
即
∴a＝4，b＝1，∴f(x)＝.
(2)∵f′(x)＝
，∴直线l的斜率k＝f′(x0)＝
，
令t＝
，t∈(0，1]，则k＝4(2t2－t)＝8
2－
，∴k∈
.∵f(x)的图象在x＝1处与直线y＝2相切，
∴
即 ∴a＝4，b＝1，∴f(x)＝.(2)∵f′(x)＝
，∴直线l的斜率k＝f′(x0)＝，令t＝
，t∈(0，1]，则k＝4(2t2－t)＝82－，∴k∈
练习册系列答案
相关题目
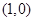的直线与曲线
和
都相切，求
的值
m(x－1)2－2x＋3＋ln x，m≥1.
时，求函数f(x)在区间[1,3]上的极小值；
的某一切线与直线
平行，则切线方程为 .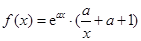
，其中
.
时，求曲线
在点
处的切线方程；
＝1，则(a－c)2＋(b－d)2的最小值为________．
在点（1,1）处的切线方程为___________.