题目内容
4.函数f(x)=ax(a>0,a≠1)在区间[1,2]上的最大值是最小值的2倍,则a的值是( )| A. | $\frac{1}{2}$或$\sqrt{2}$ | B. | $\frac{1}{2}$或2 | C. | $\frac{1}{2}$ | D. | 2 |
分析 利用指数函数的单调性,求出函数的最值,列出方程求解即可.
解答 解:由题意可得:
∵当a>1时,函数f(x)在区间[1,2]上单调递增,
∴f(2)=2f(1),
∴a2=2a,
解得a=0(舍去),或a=2.
∵当 0<a<1时,函数f(x)在区间[1,2]上单调递减,
∴f(1)=2f(2),
∴a=2a2,解得a=0(舍去),或a=$\frac{1}{2}$.
综上可得,a=2,或 a=$\frac{1}{2}$.
故选:B.
点评 本题主要考查指数函数的单调性的应用,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.奇函数f(x)(x∈R)满足f(-4)=f(1)=0,且在区间(0,2]与[2,+∞)上分别是增函数和减函数,则满足x3•f(x)>0的x的取值范围是( )
| A. | (-4,-1)∪(1,4) | B. | (-∞,4)∪(-1,0) | C. | (-∞,-4)∪(4,+∞) | D. | (-∞,-4)∪(-1,0)∪(1,4) |
19.函数$f(x)=\frac{lg(x+2)}{x+1}$的定义域是( )
| A. | (-∞,-1)∪(-1,+∞) | B. | (-2,+∞) | C. | (-2,-1)∪(-1,+∞) | D. | [-2,-1)∪(-1,+∞) |
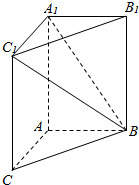 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.