题目内容
14.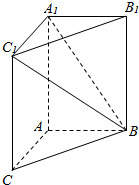 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.(1)求直线B1C1与平面A1BC1所成角的正弦值;
(2)在线段BC1上确定一点D,使得AD⊥A1B,并求$\frac{BD}{B{C}_{1}}$的值.
分析 (1)以A为原点,AC为x轴,AB为y轴,AA1为z轴,建立空间直角坐标系A-xyz,利用向量法能求出直线B1C1与平面A1BC1所成角的正弦值.
(2)设D(x,y,z)是线段BC1上一点,且$\overrightarrow{BD}=λ\overrightarrow{B{C}_{1}}$(λ∈[0,1]),利用向量法能求出在线段BC1上存在点D,使得AD⊥A1B.并能求出$\frac{BD}{B{C}_{1}}$的值.
解答  解:(1)∵AA1C1C为正方形,∴AA1⊥AC.
解:(1)∵AA1C1C为正方形,∴AA1⊥AC.
∵平面ABC⊥平面AA1C1C,
∴AA1⊥平面ABC,
∴AA1⊥AC,AA1⊥AB.
由已知AB=3,BC=5,AC=4,∴AB⊥AC.
如图,以A为原点,AC为x轴,AB为y轴,AA1为z轴,
建立空间直角坐标系A-xyz,
则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4),
∴$\overrightarrow{{A}_{1}B}$=(0,3,-4),$\overrightarrow{{A}_{1}{C}_{1}}$=(4,0,0),$\overrightarrow{{B}_{1}{C}_{1}}$=(4,-3,0).
设平面A1BC1的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}_{1}B}=3y-4z=0}\\{\overrightarrow{n}•\overrightarrow{{A}_{1}{C}_{1}}=4x=0}\end{array}\right.$,令z=3,则x=0,y=4,∴$\overrightarrow{n}$=(0,4,3).
设直线B1C1与平面A1BC1所成的角为θ,
则sinθ=|cos<$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{n}$>|=$\frac{|\overrightarrow{{B}_{1}{C}_{1}}•\overrightarrow{n}|}{|\overrightarrow{{B}_{1}{C}_{1}}|•|\overrightarrow{n}|}$=$\frac{3×4}{5×5}$=$\frac{12}{25}$.
故直线B1C1与平面A1BC1所成角的正弦值为$\frac{12}{25}$.…6分
(2)设D(x,y,z)是线段BC1上一点,且$\overrightarrow{BD}=λ\overrightarrow{B{C}_{1}}$(λ∈[0,1]),
∴(x,y-3,z)=λ(4,-3,4),
∴x=4λ,y=3-3λ,z=4λ,∴$\overrightarrow{AD}$=(4λ,3-3λ,4λ).
又$\overrightarrow{{A}_{1}B}$=(0,3,-4),由$\overrightarrow{AD}•\overrightarrow{{A}_{1}B}$=0,得3(3-3λ)-4×4λ=0,
即9-25λ=0,解得λ=$\frac{9}{25}$∈[0,1].
故在线段BC1上存在点D,使得AD⊥A1B.此时$\frac{BD}{B{C}_{1}}$=λ=$\frac{9}{25}$. …12分.
点评 本题考查线面角的正弦值的求法,考查满足条件的点是否存在的证明,是中档题,解题时要注意向量法的合理运用.

 习题精选系列答案
习题精选系列答案| A. | 1<a | B. | 1<a≤3 | C. | 1<a≤$\frac{5}{2}$ | D. | a≥3 |
| A. | [1,2] | B. | [2,8] | C. | [2,10] | D. | [1,10] |
| A. | $\frac{1}{2}$或$\sqrt{2}$ | B. | $\frac{1}{2}$或2 | C. | $\frac{1}{2}$ | D. | 2 |
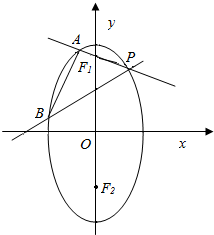 已知椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)的两个焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,直线$y=\sqrt{2}$过椭圆的焦点,点P是椭圆上位于第一象限的点,并满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=1$,过P作倾斜角互补的两条直线PA,PB分别交椭圆于A,B两点.
已知椭圆$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)的两个焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,直线$y=\sqrt{2}$过椭圆的焦点,点P是椭圆上位于第一象限的点,并满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=1$,过P作倾斜角互补的两条直线PA,PB分别交椭圆于A,B两点.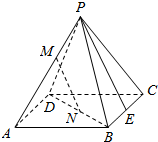 如图,已知P是正方形ABCD外一点,M,N分别是PA,BD上的点,且$\frac{PM}{MA}$=$\frac{BN}{ND}$=$\frac{1}{2}$.
如图,已知P是正方形ABCD外一点,M,N分别是PA,BD上的点,且$\frac{PM}{MA}$=$\frac{BN}{ND}$=$\frac{1}{2}$.