题目内容
9.已知A={x|m≤x≤m+1,B={x|x<-6或x>1}.(Ⅰ)若A∩B=∅,求m的取值范围;
(Ⅱ)若A∪B=B,求m的取值范围.
分析 (1)由A,B,以及A与B的交集为空集,确定出m的范围即可;
(2)由A为A与B交集的子集,确定出m范围即可.
解答 解:(Ⅰ)∵A={x|m≤x≤m+1,B={x|x<-6或x>1},且A∩B=∅,
∴$\left\{{\begin{array}{l}{m≥-6}\\{m+1≤1}\end{array}}\right.$,解得:-6≤m≤0;
(2)∵A∪B=B,
∴A⊆B,
∴m+1<-6或m>1,
解得:m<-7或m>1.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
4.函数f(x)=ax(a>0,a≠1)在区间[1,2]上的最大值是最小值的2倍,则a的值是( )
| A. | $\frac{1}{2}$或$\sqrt{2}$ | B. | $\frac{1}{2}$或2 | C. | $\frac{1}{2}$ | D. | 2 |
14.若f(x)=ax2+(2+a)x+1是偶函数,则f(x)的递增区间为( )
| A. | (-∞,0) | B. | [0,+∞) | C. | (-∞,+∞) | D. | [1,+∞) |
1.已知全集U={x∈Z|1≤x≤10},A={1,3,5,6,9,10},B={1,2,5,6,7,9,10},则A∩∁UB=( )
| A. | {1,5,6,9,10} | B. | {1,2,3,4,5,6,9,10} | ||
| C. | {7,8} | D. | {3} |
18.在△ABC中,角A、B、C的对边分别是a、b、c,则a>b是cosA<cosB的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充分且必要条件 | D. | 不充分也不必要条件 |
19.关于函数f(x)=-cos2x-($\frac{2}{3}$)|x|+$\frac{3}{2}$,有下面四个结论,其中正确结论的是( )
| A. | f(x)是奇函数 | B. | f(x)是增函数 | ||
| C. | 当x>2015时,f(x)>$\frac{1}{2}$恒成立 | D. | f(x)的最小值是-$\frac{1}{2}$. |
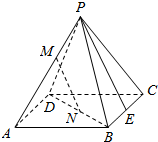 如图,已知P是正方形ABCD外一点,M,N分别是PA,BD上的点,且$\frac{PM}{MA}$=$\frac{BN}{ND}$=$\frac{1}{2}$.
如图,已知P是正方形ABCD外一点,M,N分别是PA,BD上的点,且$\frac{PM}{MA}$=$\frac{BN}{ND}$=$\frac{1}{2}$.