题目内容
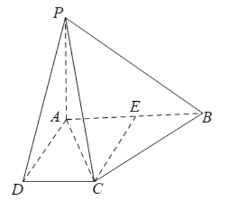
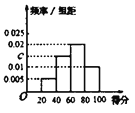
【题目】白塔中学为了解校园爱国卫生系列活动的成效，对全校学生进行了一次卫生意识测试，根据测试成绩评定“合格”“不合格”两个等级，同时对相应等级进行量化：“合格”记5分，“不合格”记0分.现随机抽取部分学生的答卷，统计结果及对应的频率分布直方图如下：
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
（1）求统计表、直方图中的a，b，c的值；
（2）用分层抽样的方法，从等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人，记所选4人的量化总分为
，求的数学期望
.
【答案】（1）18；12；0.015；（2）12.
【解析】
（1）根据得分在
的频率为：
，求出样本容量，然后可求出
的值，进一步得到
的值，然后在频率分布直方图中利用公式可求得
的值.
（2）“不合格”的学生人数为
，“合格”的学生人数为
.由题意可得
的所有可能取值为0，5，10，15，20,然后分别求出其概率，得到分布列，求出其数学期望.
解：（1）由题意知，得分在的频率为：
所以样本容量为
，
，
.
（2）“不合格”的学生人数为，“合格”的学生人数为.由题意可得的所有可能取值为0，5，10，15，20.
，
.
| 0 | 5 | 10 | 15 | 20 |
|
|
|
|
|
|
∴的分布列为：
.
【题目】某农场更新技术培育了一批新型的“盆栽果树”，这种“盆栽果树”将一改陆地栽植果树只在秋季结果的特性，能够一年四季都有花、四季都结果.现为了了解果树的结果情况，从该批果树中随机抽取了容量为120的样本，测量这些果树的高度（单位：厘米），经统计将所有数据分组后得到如图所示的频率分布直方图.
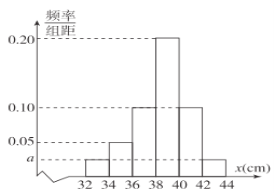
（1）求
；
（2）已知所抽取的样本来自
两个实验基地，规定高度不低于40厘米的果树为“优品盆栽”，
（i）请将图中列联表补充完整，并判断是否有
的把握认为“优品盆栽”与两个实验基地有关？
优品 | 非优品 | 合计 | |
| 60 | ||
| 20 | ||
合计 |
（ii）用样本数据来估计这批果树的生长情况，若从该农场培育的这批“盆栽果树”中随机抽取4棵，求其中“优品盆栽”的棵树
的分布列和数学期望.
附：
|
|
|
|
|
|
|
|
.
