题目内容
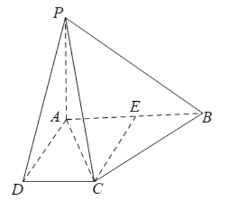
【题目】如图所示,在棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,PA=AD=DC=2,AB=4且AB∥CD,∠BAD=90°.
(1)求证:BC⊥PC;
(2)求PB与平面PAC所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题(1)连接![]() ,
,![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,所以
,所以![]() 为等腰直角三角形,故
为等腰直角三角形,故![]() ,而
,而![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .以
.以![]() 为坐标原点,
为坐标原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系,利用直线的方向向量和平面的法向量,计算得线面角的正弦值为
轴建立空间直角坐标系,利用直线的方向向量和平面的法向量,计算得线面角的正弦值为![]() .
.
试题解析:
(1)在直角梯形![]() 中,
中,![]() ,
,
取![]() 中点
中点![]() ,连接
,连接![]() ,
,
则四边形![]() 为正方形,
为正方形,
∴![]() ,
,
又![]() ,
,
则![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
由![]() 得
得![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)以![]() 为坐标原点,
为坐标原点,![]() 分别
分别![]() 为轴建立如图所示的坐标系,
为轴建立如图所示的坐标系,
则![]() ,
,![]() .
.
由(1)知![]() 即为平面
即为平面![]() 的一个法向量,
的一个法向量,
 ,
,
即![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
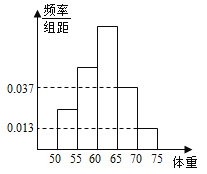
【题目】已知国家某![]() 级大型景区对拥挤等级与每日游客数量
级大型景区对拥挤等级与每日游客数量![]() (单位:百人)的关系有如下规定:当
(单位:百人)的关系有如下规定:当![]() 时,拥挤等级为“优”;当
时,拥挤等级为“优”;当![]() 时,拥挤等级为“良”;当
时,拥挤等级为“良”;当![]() 时,拥挤等级为“拥挤”;当
时,拥挤等级为“拥挤”;当![]() 时,拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据:
时,拥挤等级为“严重拥挤”.该景区对6月份的游客数量作出如图的统计数据:
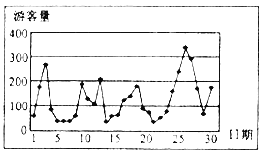
(1)下面是根据统计数据得到的频率分布表,求出![]() 的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
游客数量(单位:百人) |
|
|
|
|
天数 |
| 10 | 4 | 1 |
频率 |
|
|
|
|
(2)某人选择在6月1日至6月5日这5天中任选2天到该景区游玩,求他这2天遇到的游客拥挤等级均为“优”的频率.