题目内容
13.把下列复数表示成三角形式:-$\frac{1}{2}-\frac{\sqrt{3}}{2}$i.
分析 求出模及幅角,即可将复数的代数形式化为三角形式.
解答 解:-$\frac{1}{2}-\frac{\sqrt{3}}{2}$i=cos$\frac{4π}{3}$+isin$\frac{4π}{3}$
点评 本题考查复数的代数形式化为三角形式,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
18.已知△ABC是半径为5的圆O的内接三角形,且$tanA=\frac{4}{3}$,若$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}(x、y∈R)$,则x+y的最大值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | 1 | D. | $\frac{5}{8}$ |
2.若函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+(a-1)x+1在区间(1,4)上为减函数,在区间(6,+∞)上为增函数,则实数a的取值范围为( )
| A. | (-∞,0] | B. | [-1,3] | C. | [3,5] | D. | [5,7] |
3.执行如图所示的程序框图,若输入x=30,则输出的结果为( )
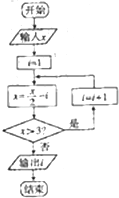

| A. | 4 | B. | 3 | C. | 2 | D. | 1 |