题目内容
2.若函数f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+(a-1)x+1在区间(1,4)上为减函数,在区间(6,+∞)上为增函数,则实数a的取值范围为( )| A. | (-∞,0] | B. | [-1,3] | C. | [3,5] | D. | [5,7] |
分析 求出原函数的导函数,求得导函数的零点1,a-1,然后分1与a-1的大小分析导函数在不同区间内的符号,从而得到原函数在不同区间内的单调性,最后借助于已知条件得到a-1与4和6的关系,则答案可求.
解答 解:由f(x)=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+(a-1)x+1,得
f′(x)=x2-ax+a-1,
令f′(x)=0,解得x=1或x=a-1.
当a-1≤1,即a≤2时,f′(x)在(1,+∞)上大于0,函数f(x)在(1,+∞)上为增函数,不合题意;
当a-1>1,即a>2时,f′(x)在(-∞,1)上大于0,函数f(x)在(-∞,1)上为增函数,
f′(x)在(1,a-1)内小于0,函数f(x)在(1,a-1)内为减函数,f′(x)在(a-1,+∞)内大于0,
函数f(x)在(a-1,+∞)上为增函数.
依题意应有:
当x∈(1,4)时,f′(x)<0,
当x∈(6,+∞)时,f′(x)>0.
∴4≤a-1≤6,解得5≤a≤7.
∴aa的取值范围是[5,7].
故选:D.
点评 本题考查了利用导数研究函数的单调性,考查了分类讨论的数学思想方法,采用了逆向思维方法,解答的关键是对端点值的取舍,是中档题.

练习册系列答案
相关题目
17.执行如图所示的程序框图,若输出的结果是$\frac{12}{13}$,则循环体的判断框内①处应填( )


| A. | 11? | B. | 12? | C. | 13? | D. | 14? |
12.已知点P(x,y)在曲线$\left\{\begin{array}{l}x=-2+cosθ\\ y=sinθ\end{array}\right.$(θ为参数,且θ∈[π,2π))上,则点P到直线$\left\{\begin{array}{l}x=2+t\\ y=-1-t\end{array}\right.(t$为参数)的距离的取值范围是( )
| A. | [-$\frac{{3\sqrt{2}}}{2}$,$\frac{{3\sqrt{2}}}{2}$] | B. | [$\frac{{3\sqrt{2}}}{2}$-1,$\frac{{3\sqrt{2}}}{2}$+1] | C. | ($\sqrt{2}$,2$\sqrt{2}$] | D. | ($\sqrt{2}$,$\frac{{3\sqrt{2}}}{2}$+1] |
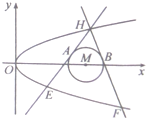 已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.
已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.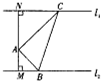 如图,A是两条平行直线之间的一定点,且点A到两条平行直线的距离分别为AM=1,AN=$\sqrt{3}$.设△ABC,AC⊥AB,且顶点B、C分别在两条平行直线上运动,则$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$的最大值为$\sqrt{2}$.
如图,A是两条平行直线之间的一定点,且点A到两条平行直线的距离分别为AM=1,AN=$\sqrt{3}$.设△ABC,AC⊥AB,且顶点B、C分别在两条平行直线上运动,则$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$的最大值为$\sqrt{2}$.