题目内容
18.已知△ABC是半径为5的圆O的内接三角形,且$tanA=\frac{4}{3}$,若$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}(x、y∈R)$,则x+y的最大值为( )| A. | $\frac{4}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | 1 | D. | $\frac{5}{8}$ |
分析 延长AO与BC相交于点D,作OA1∥DA2∥AB,OB1∥DB2∥AC,设$\overrightarrow{AD}=m\overrightarrow{AB}+n\overrightarrow{AC}(m>0,n>0)$,推出$\frac{m}{x}=\frac{n}{y}=\frac{|AD|}{|AO|}$,结合B、D、C三点共线,得到x+y的表达式,利用三角代换,求解最值即可.
解答 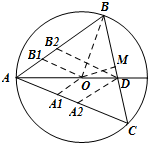 解:延长AO与BC相交于点D,作OA1∥DA2∥AB,OB1∥DB2∥AC,
解:延长AO与BC相交于点D,作OA1∥DA2∥AB,OB1∥DB2∥AC,
设$\overrightarrow{AD}=m\overrightarrow{AB}+n\overrightarrow{AC}(m>0,n>0)$,易知x>0,y>0,则$\frac{m}{x}=\frac{n}{y}=\frac{{|{AD}|}}{{|{AO}|}}⇒$$\left\{\begin{array}{l}m=\frac{{|{AD}|}}{{|{AO}|}}x\\ n=\frac{{|{AD}|}}{{|{AO}|}}y\end{array}\right.⇒\overrightarrow{AD}=x•\frac{{|{AD}|}}{{|{AO}|}}\overrightarrow{AB}+y•\frac{{|{AD}|}}{{|{AO}|}}\overrightarrow{AC}$,
又B、D、C三点共线,所以$x•\frac{{|{AD}|}}{{|{AO}|}}+y•\frac{{|{AD}|}}{{|{AO}|}}=1⇒x+y=\frac{{|{AO}|}}{{|{AD}|}}=\frac{AO}{AO+OD}=\frac{1}{{1+\frac{OD}{AO}}}$,
只需$\frac{OD}{AO}$最小,就能使x+y最大,所以当OD最小即可,过点O作OM⊥BC于点M,从而OD≥OM,
又∠BOM=∠BAC=θ,由$tanθ=\frac{4}{3}⇒cosθ=\frac{3}{5}=\frac{OM}{OB}⇒OM=3$,
那么$x+y≤\frac{1}{{1+\frac{3}{5}}}=\frac{5}{8}$.
故选:D.
点评 本题考查向量在集合中的应用,三角代换以及共线向量的应用,是中档题.

| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
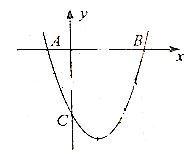 如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.
如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.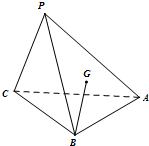 点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心.
点P是△ABC所在的平面外一点P,连结PA、PB、PC,且有PB=PC=$\sqrt{5}$,AB=AC=2$\sqrt{2}$,∠BAC=90°,G为△PAB的重心.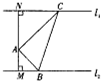 如图,A是两条平行直线之间的一定点,且点A到两条平行直线的距离分别为AM=1,AN=$\sqrt{3}$.设△ABC,AC⊥AB,且顶点B、C分别在两条平行直线上运动,则$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$的最大值为$\sqrt{2}$.
如图,A是两条平行直线之间的一定点,且点A到两条平行直线的距离分别为AM=1,AN=$\sqrt{3}$.设△ABC,AC⊥AB,且顶点B、C分别在两条平行直线上运动,则$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$的最大值为$\sqrt{2}$.