题目内容
7.已知函数f(x)=2$\sqrt{3}sinxcosx+2{cos^2}$x(x∈R).(Ⅰ)求函数f(x)的最小正周期及在区间$[{0,\frac{π}{2}}]$上的最大值和最小值;
(Ⅱ)将函数f(x)图象向左平移$\frac{π}{6}$个单位,再向上平移1个单位,得到函数g(x)图象,求g(x)的对称轴方程和对称中心坐标.
分析 (Ⅰ)由三角函数中的恒等变换应用化简函数解析式可得$f(x)=2sin(2x+\frac{π}{6})+1$,根据x的范围和正弦函数的极值性即可得解;
(Ⅱ)由三角函数图形变换规律可求g(x),由2x=kπ,(k∈Z)可得对称轴,由2x=k$π+\frac{π}{2}$,(k∈Z)可得对称中心.
解答 解:(Ⅰ)∵f(x)=2$\sqrt{3}sinxcosx+2{cos^2}$x=$\sqrt{3}$sin2x+1+cos2x,
∴$f(x)=2sin(2x+\frac{π}{6})+1$,
∵$x∈[0,\frac{π}{2}]$,
∴$2x+\frac{π}{6}∈[\frac{π}{6},\frac{7π}{6}]$,
∴f(x)的最大值为3--------------(6分)
(Ⅱ)∵$f(x)=2sin(2x+\frac{π}{6})+1$,将函数f(x)图象向左平移$\frac{π}{6}$个单位,再向上平移1个单位,得到函数g(x)图象,
∴g(x)=2cos2x+2,
∴由2x=kπ,(k∈Z)可得对称轴为直线$x=\frac{kπ}{2}$,(k∈Z)
由2x=k$π+\frac{π}{2}$,(k∈Z)可得对称中心为$(\frac{π}{4}+\frac{kπ}{2},2)$,(k∈Z)--------(12分)
点评 本题主要考查了三角函数中的恒等变换应用,三角函数图形变换规律,正弦函数,余弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
17.设变量x、y满足约束条件$\left\{\begin{array}{l}x+y≤3\\ x-y≥-1\\ y≥1\end{array}\right.$,则目标函数z=-2x+y的最大值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
15.在各项均为正数的等比数列{an}中,已知a1a5=25,则a3等于( )
| A. | 5 | B. | 25 | C. | -25 | D. | -5或5 |
12.“a≥3”是“?x∈[1,2],使得x2-a≤0”的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
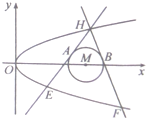 已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.
已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.