题目内容
1．已知点P（2，6）和圆x2+y2+2x-4y-4=0，解答下列问题：（1）求圆心和半径；
（2）判断点P是否在圆上；
（3）求圆上的点到点P的最长距离和最短距离．
分析 （1）圆x2+y2+2x-4y-4=0，化为标准方程，即可求圆心和半径；
（2）利用22+62+4-24-4＞0，判断点P是否在圆上；
（3）求出PC，即可求圆上的点到点P的最长距离和最短距离．
解答 解：（1）圆x2+y2+2x-4y-4=0，化为标准方程为圆（x+1）2+（y-2）2=9，圆心C（-1，2），半径r=3；
（2）因为22+62+4-24-4＞0，所以点P不在圆上，在圆外；
（3）PC=$\sqrt{（2+1）^{2}+（6-2）^{2}}$=5，
所以圆上的点到点P的最长距离为8，最短距离为2．
点评 本题考查圆的方程，考查点与圆的位置关系，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
15．在各项均为正数的等比数列{an}中，已知a1a5=25，则a3等于（ ）
| A． | 5 | B． | 25 | C． | -25 | D． | -5或5 |
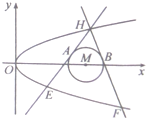已知抛物线C：y2=2px（p＞0）和⊙M：（x-4）2+y2=r2（0＜r≤1），圆心M到抛物线C的准线的距离为$\frac{17}{4}$，过抛物线C上一点H（x0，y0）（y0≥1）作两条直线分别与⊙M相切与A、B两点，与抛物线C交于E、F两点．
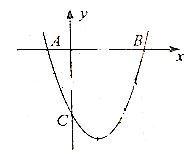如图，已知二次函数y=ax2+bx-3的图象过坐标（-2，5），与x轴的两个交点分别为A，B（3，0）．与y轴的负半轴交于点C．
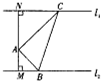如图，A是两条平行直线之间的一定点，且点A到两条平行直线的距离分别为AM=1，AN=$\sqrt{3}$．设△ABC，AC⊥AB，且顶点B、C分别在两条平行直线上运动，则$\frac{1}{AB}$+$\frac{\sqrt{3}}{AC}$的最大值为$\sqrt{2}$．