题目内容
4.已知函数f(x)=sin2x-$\sqrt{3}$cos2x-a.(1)若f(x)在[0,$\frac{π}{3}$]上的最大值为3,求实数a的值;
(2)若f(x)在[$\frac{π}{4}$π]上只有一个零点,求实数a的取值范围.
分析 (1)f(x)=2sin(2x-$\frac{π}{3}$)-a,根据-$\frac{π}{3}$≤x-$\frac{π}{3}$≤$\frac{π}{3}$,即$-\sqrt{3}$≤2sin(2x-$\frac{π}{3}$)$≤\sqrt{3}$求解.
(2)f(x)在[$\frac{π}{4}$π]上只有一个零点,得出y=2sin(2x-$\frac{π}{3}$)与y=a,在[$\frac{π}{4}$π]上只有一个交点,
运用图象判断范围.
解答 解:∵f(x)=sin2x-$\sqrt{3}$cos2x-a.
∴f(x)=2sin(2x-$\frac{π}{3}$)-a,
(1)∵x∈[0,$\frac{π}{3}$],
∴-$\frac{π}{3}$≤x-$\frac{π}{3}$≤$\frac{π}{3}$,
即$-\sqrt{3}$≤2sin(2x-$\frac{π}{3}$)$≤\sqrt{3}$的最大值为$\sqrt{3}-a$.
∵f(x)在[0,$\frac{π}{3}$]上的最大值为3,
∴$\sqrt{3}-a$=3,a=$\sqrt{3}-3$.
(2)∵x∈[$\frac{π}{4}$π],
∴$\frac{π}{6}$≤2x$-\frac{π}{3}$≤$\frac{5π}{3}$
∵f(x)在[$\frac{π}{4}$π]上只有一个零点,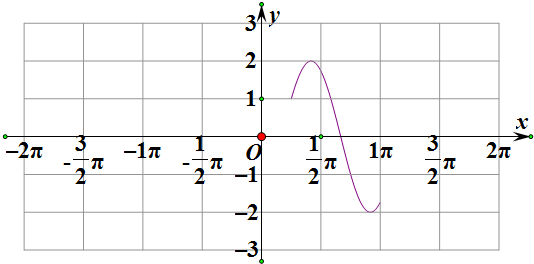
∴y=2sin(2x-$\frac{π}{3}$)与y=a,在[$\frac{π}{4}$π]上只有一个交点,
∴a=2或-$\sqrt{3}$<a<1,或a=-2,
点评 本题考查了三角变换及三角函数的图象与性质,解题的关键是把函数化成正弦型函数的标准形式,利用单调性求解,关键是画出图象判断即可.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
19.设F(c,0)为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点,点B的坐标为(0,b).若圆(x-c)2+y2=r2(r>0)与双曲线的渐近线相切,且|FB|≥$\sqrt{3}$r,则该双曲线的离心率e的取值范围是( )
| A. | $(1,\sqrt{2}]$ | B. | $[\sqrt{2},+∞)$ | C. | $(1,\sqrt{3}]$ | D. | $[\sqrt{3},+∞)$ |
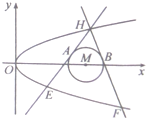 已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.
已知抛物线C:y2=2px(p>0)和⊙M:(x-4)2+y2=r2(0<r≤1),圆心M到抛物线C的准线的距离为$\frac{17}{4}$,过抛物线C上一点H(x0,y0)(y0≥1)作两条直线分别与⊙M相切与A、B两点,与抛物线C交于E、F两点.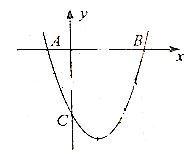 如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.
如图,已知二次函数y=ax2+bx-3的图象过坐标(-2,5),与x轴的两个交点分别为A,B(3,0).与y轴的负半轴交于点C.