题目内容
12.设函数f(x)=ax+ka-x(a>0,且a≠1)是定义域为R的奇函数.(1)求实数k的值;
(2)若f(1)=$\frac{3}{2}$.求证:f(x)是单调增函数.
分析 (1)由于函数f(x)=ax+ka-x(a>0,且a≠1)是定义域为R的奇函数,得f(-x)+f(x)=0对于任意实数都成立.即可得出k.
(2)由(1)可知:f(x)=ax-a-x,利用f(1)=a-a-1=$\frac{3}{2}$.又a>0,解得a=2,可得f(x)=2x-2-x.任取实数x1<x2,只要证明f(x1)-f(x2)<0即可;
解答 解:(1)∵函数f(x)=ax+ka-x(a>0,且a≠1)是定义域为R的奇函数,
∴f(-x)+f(x)=a-x+kax+ax+ka-x=(k+1)(ax+a-x)=0对于任意实数都成立.
∴k=-1.
(2)由(1)可知:f(x)=ax-a-x,
∵f(1)=a-a-1=$\frac{3}{2}$,又a>0,解得a=2.
∴f(x)=2x-2-x.
任取实数x1<x2,则f(x1)-f(x2)=2${\;}^{{x}_{1}}$-2${\;}^{-{x}_{1}}$-(2${\;}^{{x}_{2}}$-2${\;}^{-{x}_{2}}$)
=(2${\;}^{{x}_{1}}$$-{2}^{{x}_{2}}$)(1$+\frac{1}{{2}^{{x}_{1}+{x}_{2}}}$),
∵x1<x2,∴2${\;}^{{x}_{1}}$<2${\;}^{{x}_{2}}$,又2${\;}^{{x}_{1}+{x}_{2}}$>0,
∴f(x1)<f(x2),∴f(x)是单调增函数;
点评 本题考查了函数的单调性、奇偶性、二次函数的单调性,属于中档题

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
20.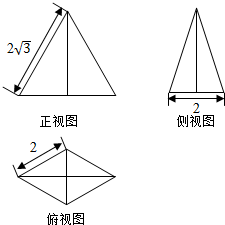 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 4$\sqrt{3}$ | D. | 2 |
7.不等式$\frac{2-x}{x-4}≤0$的解集为( )
| A. | {x|-2≤x<4} | B. | {x|x≤2} | C. | {x|x>-4} | D. | {x|x≤2或x>4} |
17.直线l经过点(1,2),且倾斜角是直线y=x倾斜角的2倍,则以下各点在直线l上的是( )
| A. | (1,1) | B. | (2,2) | C. | (2,1) | D. | (2,0) |
1.已知集合$A=(-∞,\frac{1}{2}]$,函数y=ln(2x+1)的定义域为集合B,则A∩B=( )
| A. | $({-\frac{1}{2},\frac{1}{2}}]$ | B. | $({-\frac{1}{2},\frac{1}{2}})$ | C. | $({-∞,-\frac{1}{2}})$ | D. | $[{\frac{1}{2},+∞})$ |