题目内容

7．求经过直线l1：3x+2y-5=0，l2：3x-2y-1=0的交点且平行于直线2x+y-5=0的直线方程．

分析 联立$\left\{\begin{array}{l}{3x+2y-5=0}\\{3x-2y-1=0}\end{array}\right.$，解得交点坐标（1，1），与直线2x+y-5=0平行的直线为：2x+y+m=0，把（1，1）代入解得即可．

解答 解：联立$\left\{\begin{array}{l}{3x+2y-5=0}\\{3x-2y-1=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$，交点坐标（1，1）．
与直线2x+y-5=0平行的直线为：2x+y+m=0，把（1，1）代入可得2+1+m=0，解得m=-3．
∴所求的直线方程为：2x+y-3=0．

点评 本题考查了直线的交点坐标、平行线的斜率之间的关系，考查了计算能力，属于基础题．

练习册系列答案
相关题目
17．图中所示算法流程图的功能是（　　）
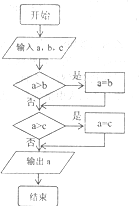
A．求a、b、c三数的最大数B．求a、b、c三数的最小数
C．将a、b、c三数由大到小排列D．将a、b、c三数由小到大排列
18．在△ABC中，若∠A=60°，∠B=45°，BC=3$\sqrt{2}$，则AC等于（　　）
A．4$\sqrt{3}$B．$\frac{\sqrt{3}}{2}$C．$\sqrt{3}$D．2$\sqrt{3}$
15．△ABC外接圆的圆心O，半径为1，若$\overrightarrow{AB}+\overrightarrow{AC}$=2$\overrightarrow{AO}$，且|$\overrightarrow{AC}$|=|$\overrightarrow{AO}$|，则向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为（　　）
A．$\frac{3}{2}$B．-$\frac{\sqrt{3}}{2}$C．$\frac{\sqrt{3}}{2}$D．-$\frac{3}{2}$
2．已知$\overrightarrow{a}$=（cosωx，sinωx），$\overrightarrow{b}$=（cosωx，-$\sqrt{3}$cosωx），函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$-$\frac{1}{2}$，若直线x=$\frac{π}{3}$是y=f（x）图象的一条对称轴．
（1）求正数ω的最小值；
（2）当正数ω取最小值时，求函数f（x）的单调区间．
12．设向量$\overline a=（1，2），\overrightarrow b=（m，m+1），\overrightarrow a⊥\overrightarrow b$，则实数m的值为（　　）
A．0B．-$\frac{2}{3}$C．-$\frac{9}{5}$D．-3
19．将函数f（x）=cos2x的图象横坐标不变纵坐标伸长到原来的2倍，再向左平移$\frac{π}{6}$个单位后，得到函数g（x）的图象，则$g（\frac{π}{6}）$=-1．
16．已知函数y=f（x）是定义域为R的奇函数．当x≥0时f（x）=$\left\{{\begin{array}{l}{{x^2}，0≤x≤1}\\{f（x-1）+1，x＞1}\end{array}}\right.$．若恰有5个不同的实数x1，x2，…，x5，使得f（x）=mx成立，则实数m的值为（　　）
A．$\sqrt{2}$-1B．2$\sqrt{2}$-2C．2-$\sqrt{2}$D．3-2$\sqrt{2}$
5．正四面体ABCD中，M，N分别是棱BC和棱AC的中点，则异面直线AM和DN所成的角的余弦值为（　　）
A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{6}$D．0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网