题目内容
2.已知$\overrightarrow{a}$=(cosωx,sinωx),$\overrightarrow{b}$=(cosωx,-$\sqrt{3}$cosωx),函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$-$\frac{1}{2}$,若直线x=$\frac{π}{3}$是y=f(x)图象的一条对称轴.(1)求正数ω的最小值;
(2)当正数ω取最小值时,求函数f(x)的单调区间.
分析 (1)由题意可得f(x)=cos(2ωx+$\frac{π}{3}$),由三角函数的对称性易得正数ω取最小值;
(2)可得f(x)=cos(2x+$\frac{π}{3}$),解不等式2kπ≤2x+$\frac{π}{3}$≤2kπ+π可得单调递减区间,同理可得单调递增区间.
解答 解:(1)由题意可得f(x)=$\overrightarrow{a}•\overrightarrow{b}$-$\frac{1}{2}$
=cos2ωx-$\sqrt{3}$sinωxcosωx-$\frac{1}{2}$
=$\frac{1}{2}$(1+cos2ωx)-$\frac{\sqrt{3}}{2}$sin2ωx-$\frac{1}{2}$
=$\frac{1}{2}$cos2ωx-$\frac{\sqrt{3}}{2}$sin2ωx
=cos(2ωx+$\frac{π}{3}$),
∵直线x=$\frac{π}{3}$是y=f(x)图象的一条对称轴,
∴2ω•$\frac{π}{3}$+$\frac{π}{3}$=kπ,k∈Z,
∴ω=$\frac{3}{2}$k-$\frac{1}{2}$,k∈Z,
∴当k=1时,正数ω取最小值1;
(2)当正数ω取最小值1时,f(x)=cos(2x+$\frac{π}{3}$),
由2kπ≤2x+$\frac{π}{3}$≤2kπ+π可得kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,
∴函数f(x)的单调递减区间为[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z;
同理可得函数f(x)的单调递增区间为[kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$],k∈Z.
点评 本题考查三角函数的最值和单调性,涉及三角函数的对称性,属基础题.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案 如图所示,将n2(n≥9)个正数排成n行n列的数阵,其中的每一行都成等差数列,每一列都成等比数列,各等比数列的公比都相同且不为1,若a11=a22=a34=$\frac{1}{2}$,则a11+a22+a33+…+a99=( )
如图所示,将n2(n≥9)个正数排成n行n列的数阵,其中的每一行都成等差数列,每一列都成等比数列,各等比数列的公比都相同且不为1,若a11=a22=a34=$\frac{1}{2}$,则a11+a22+a33+…+a99=( )| A. | $\frac{1031}{512}$ | B. | $\frac{1031}{512}$ | C. | $\frac{1013}{1024}$ | D. | $\frac{1031}{1024}$ |
| A. | $[-\frac{3}{2}π,π]$ | B. | $[\frac{5}{2}π,3π]$ | C. | $[-\frac{5}{6}π,-\frac{π}{2}]$ | D. | $[-\frac{1}{2}π,\frac{5π}{2}]$ |
| A. | (-$\frac{1}{3}$,$\frac{1}{3}$) | B. | [-$\frac{1}{3}$,$\frac{1}{3}$] | C. | ($\frac{2}{3}$,$\frac{4}{3}$) | D. | [$\frac{2}{3}$,$\frac{4}{3}$] |
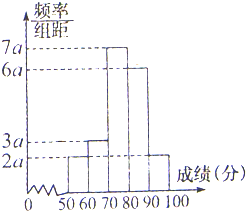 200名学生,某次数学考试成绩(单位:分)的频率分布直方图如图所示:
200名学生,某次数学考试成绩(单位:分)的频率分布直方图如图所示: