题目内容
15.△ABC外接圆的圆心O,半径为1,若$\overrightarrow{AB}+\overrightarrow{AC}$=2$\overrightarrow{AO}$,且|$\overrightarrow{AC}$|=|$\overrightarrow{AO}$|,则向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为( )| A. | $\frac{3}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{3}{2}$ |
分析 利用向量加法的几何意义 得出△ABC是以A为直角的直角三角形.继而求出向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影.
解答 解:∵$\overrightarrow{AB}+\overrightarrow{AC}$=2$\overrightarrow{AO}$,
∴($\overrightarrow{AB}$-$\overrightarrow{AO}$)+($\overrightarrow{AC}$-$\overrightarrow{AO}$)=$\overrightarrow{OB}$+$\overrightarrow{OC}$=0,
所以BC为圆O的直径.又|$\overrightarrow{AC}$|=|$\overrightarrow{AO}$|=1,
所以∠C=60°,∠B=30°,|$\overrightarrow{BA}$|=$\sqrt{3}$,
所以向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为|$\overrightarrow{BA}$|cosB=$\frac{3}{2}$.
故选:A.
点评 本题考查向量加法的几何意义,向量投影的计算.得出△ABC是以A为直角的直角三角形是关键,属于中档题.

练习册系列答案
相关题目
5.定积分$\int_0^1{(2x-{e^x})}$dx的值为( )
| A. | 2-e | B. | -e | C. | e | D. | 2+e |
3.要从编号为1,2,3…,60的某种型号冰箱中随机抽取6台进行检测,用系统抽样的方法确定所选取的6台冰箱的编号可能是( )
| A. | 5,10,15,20,25,30 | B. | 3,13,23,33,43,53 | ||
| C. | 1,2,3,4,5,6 | D. | 2,4,8,16,32,48 |
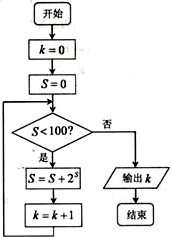
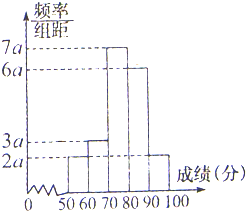 200名学生,某次数学考试成绩(单位:分)的频率分布直方图如图所示:
200名学生,某次数学考试成绩(单位:分)的频率分布直方图如图所示: