题目内容
18．在△ABC中，若∠A=60°，∠B=45°，BC=3$\sqrt{2}$，则AC等于（ ）| A． | 4$\sqrt{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
分析 由正弦定理可得：$\frac{AC}{sin4{5}^{°}}=\frac{3\sqrt{2}}{sin6{0}^{°}}$，解出即可．
解答 解：由正弦定理可得：$\frac{AC}{sin4{5}^{°}}=\frac{3\sqrt{2}}{sin6{0}^{°}}$，
解得AC=$\frac{3\sqrt{2}sin4{5}^{°}}{sin6{0}^{°}}$=2$\sqrt{3}$．
故选：D．
点评 本题考查了正弦定理解三角形，属于基础题．
练习册系列答案
相关题目
3．要从编号为1，2，3…，60的某种型号冰箱中随机抽取6台进行检测，用系统抽样的方法确定所选取的6台冰箱的编号可能是（ ）
| A． | 5，10，15，20，25，30 | B． | 3，13，23，33，43，53 | ||
| C． | 1，2，3，4，5，6 | D． | 2，4，8，16，32，48 |
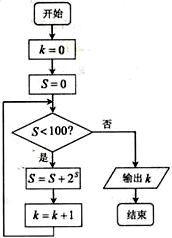
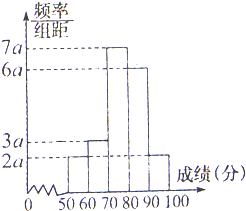200名学生，某次数学考试成绩（单位：分）的频率分布直方图如图所示：