题目内容
12．设向量$\overline a=（1，2），\overrightarrow b=（m，m+1），\overrightarrow a⊥\overrightarrow b$，则实数m的值为（ ）| A． | 0 | B． | -$\frac{2}{3}$ | C． | -$\frac{9}{5}$ | D． | -3 |
分析 由条件利用两个向量的数量积公式，两个向量垂直的性质，求得实数m的值．
解答 解：由向量$\overline a=（1，2），\overrightarrow b=（m，m+1），\overrightarrow a⊥\overrightarrow b$，
可得m+2（m+1）=0，求得m=-$\frac{2}{3}$，
故选：B．
点评 本题主要考查两个向量的数量积公式，两个向量垂直的性质，属于基础题．
练习册系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
3．要从编号为1，2，3…，60的某种型号冰箱中随机抽取6台进行检测，用系统抽样的方法确定所选取的6台冰箱的编号可能是（ ）
| A． | 5，10，15，20，25，30 | B． | 3，13，23，33，43，53 | ||
| C． | 1，2，3，4，5，6 | D． | 2，4，8，16，32，48 |
17．
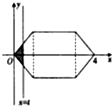如图所示的图形由两个等腰直角三角形和一个正方形组成，且正方形的边长为2，直线x=t（0＜t≤4）从左到右扫过图形的面积为S=f（t），则$f（\frac{1}{4}）+f（\frac{3}{2}）$等于（ ）
如图所示的图形由两个等腰直角三角形和一个正方形组成，且正方形的边长为2，直线x=t（0＜t≤4）从左到右扫过图形的面积为S=f（t），则$f（\frac{1}{4}）+f（\frac{3}{2}）$等于（ ）| A． | $\frac{11}{4}$ | B． | $\frac{9}{4}$ | C． | $\frac{29}{16}$ | D． | $\frac{33}{16}$ |